Multi-objective optimization in the asynchronous island model

PyGMO can be used to optimize problems with more than one objective. While the general workflow is similar to single-objective optimization, there are some more features like plotting that can be used to analyse the process. In order to plot, start an ipython-shell with matplotlib activated:

ipython --pylab

Let us now initialize a multi-objective problem of the ZDT test suite and solve it with an multi-objective optimization algorithm.

from PyGMO import *
prob = problem.zdt(3)
alg = algorithm.nsga_II(gen = 1)
pop = population(prob, 200)
for i in xrange(200):
    pop = alg.evolve(pop)
pop.plot_pareto_fronts()

The last call draws you a nice plot of the population and the obtained Pareto-front and is especially useful for problems with two objectives.

You can also investigate a list of the non-dominated fronts the algorithm produces by using the following command. In this example it should give you just one front back, since all individuals are non-dominated by now.

pop.compute_pareto_fronts()

Try this command on a newly initialized population and you will see different non-dominated fronts, ordered from first to the last.

Of course, you can also use the whole power of the underlying asynchronous island model of PyGMO to optimize your problems. Let us solve a problem with three objective with the help of an archipelago, consisting of 16 islands, each containing just 32 individuals.

prob = problem.dtlz(3)
alg = algorithm.nsga_II(gen = 1)
s_pol = migration.best_s_policy(0.1, migration.rate_type.fractional)
r_pol = migration.fair_r_policy(0.1, migration.rate_type.fractional)
archi = archipelago(topology=topology.fully_connected())
isls = [island(alg, prob, 32, s_policy=s_pol, r_policy=r_pol) for i in xrange(16)]
for isl in isls:
    archi.push_back(isl)

In this setting, we migrate the 10% best individuals of each island and replace 10% of the old population (if the new migrants are not worse). However, the meaning of “best” and “worst” is different compared to single-objective optimization. PyGMO is using the crowded comparison operator internally to order all individuals in a multi-objective population. This ordering favours at first members with low non-domination ranks and, if individuals belong to the same front, members with the highest crowding distance (thus individuals in sparsely populated areas of the fitness space). Thus, there is a notion of a champion for PyGMO in the multi-objective setting: it is the individual with the best non-domination rank (being in the non-dominated front) with the highest crowding distance. The following command gives us the best 3 individuals of every island in the archipelago

for isl in archi:
    print isl.population.get_best_idx(3)

For a single individual of a population we can also query by how many individuals it is dominated (domination count) and which individuals it dominates by itself (domination list):

[archi[0].population.get_domination_list(i) for i in xrange(32)]
[archi[0].population.get_domination_count(i) for i in xrange(32)]

Lets evolve the archipelago for 500 generations.

for i in xrange(500):
     archi.evolve(1)

We will now create a new population that consists of all the individuals of the archipelago. Since the plotting-function of the population itself is limited to 2D-plotting, we will use the plotting function of the problem itself, which provides a 3D plot with the actual Pareto-front highlighted blue.

pop = population(prob)
for isl in archi:
    for ind in isl.population:
        pop.push_back(ind.cur_x)
prob.plot(pop)

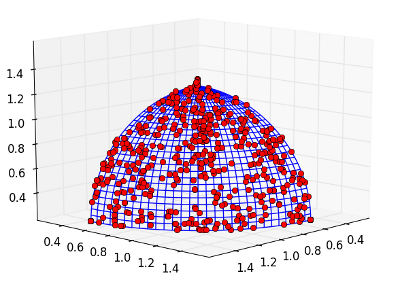
Obtaining the same amount of solutions (which is 512 in this example) takes significantly more time if one uses just a single, large population. Moreover, there is evidence that migration in multi-objective optimization helps to reduce the number of generations needed and helps algorithms to better explore the whole Pareto-front.