Using homotopy and Pontryagin to refine solutions from the direct method - Part I¶

These plots are produced by the following code:

import pykep as pk
pk.examples.run_example9()

if snopt7 is not available, ipopt or slsqp will also produce, eventually, a feasible solution.

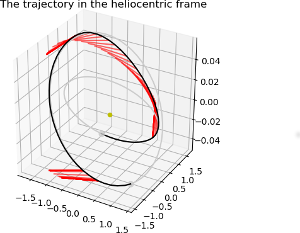
This example demonstrates the use of the pykep.trajopt.indirect_pt2pl which represents, in cartesian coordinates, the TPBVP problem resulting from applying Pontryagin maximum principle to the dynamics of a mass varying spacecraft. The starting conditions are fixed and were obtained running a direct method first (see previous example). The end condition is a Mars randezvous. Since the corresponding transversality condition (free time, Mars randezvous) is tricky to write for a generic pykep.planet._base, we hybridize the indirect method with a direct approach. We ignore the transversality conditions when computing the Pontryagin leg, but we add as criteria the optimization of the final mass to be passed directly to the solver.

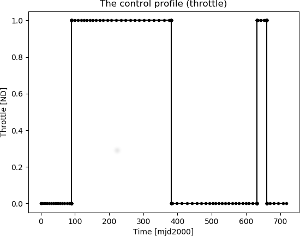
Note that the control structure is off bang off bang with a final ballistic arc which is irrelevant since the planet has been met a few days before already.

The code for this example can be studied here. Feel free to leave comments.