ML-dSGP4

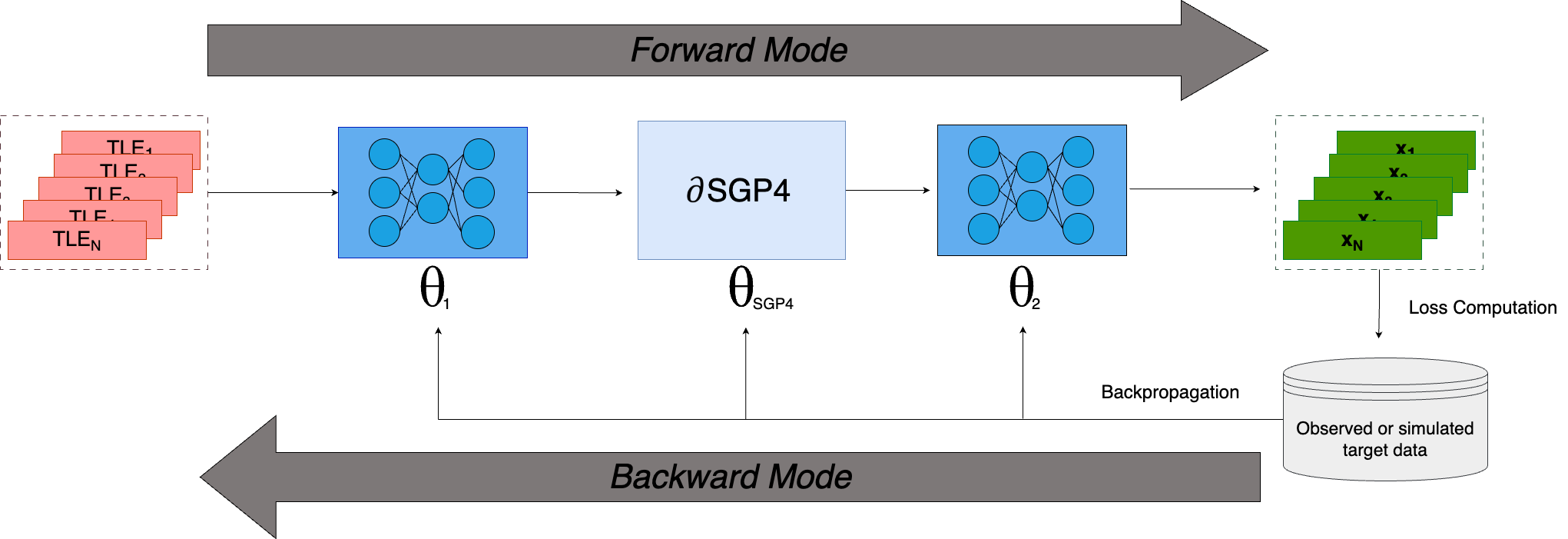
This tutorial introduces a hybrid model that uses neural networks to correct the input and outputs of dSGP4, to better match the precision of high-precision numerical integrators and/or simulated data.

For more details on what this entails and some discussion on the obtained results on <2,000 Starlink satellites, check out our publication: Acciarini, Giacomo, Atılım Güneş Baydin, and Dario Izzo. “Closing the Gap Between SGP4 and High-Precision Propagation via Differentiable Programming” (2024) Vol. 226(1), pages: 694-701.

The objective is to provide a way to improve the dSGP4 accuracy, when higher-precision simulated or observed data is available. This could also be a powerful tool for operators.

For this, we leverage the differentiablity of dSGP4 to backpropagate through inputs and outputs of the model.

Imports

import dsgp4
import torch
import matplotlib.pyplot as plt

Load TLEs and ML-dSGP4 pre-trained model:

#we load some TLEs, as usual:
tles = dsgp4.tle.load("example.tle")

#we load a pre-trained ML-dSGP4 model:
ml_dsgp4=dsgp4.mldsgp4(hidden_size=35)
ml_dsgp4.load_model(path='mldsgp4_example_model.pth',device='cpu')

💡 Note: the output is normalized, and the normalization constant can be defined through normalization_R and normalization_V argumnets in dsgp4.mldsgp4, if not defined, default will be used.

Prepare data

#we now create a batch of TLE to later propagate it
tles_=[]
for tle in tles:
    tles_+=[tle]*10000
tsinces = torch.cat([torch.linspace(0,24*60,10000)]*len(tles))

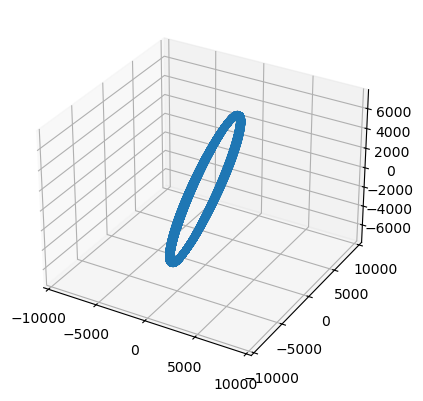
Batch TLE Propagation with ML-dSGP4

#we use torch.no_grad() to avoid keeping track of the derivatives:
with torch.no_grad():    
    states_normalized_out=ml_dsgp4(tles_,tsinces)
states_normalized_out=states_normalized_out.detach().clone().numpy()

#if we want to unnormalize:
position=states_normalized_out[:,:3]*ml_dsgp4.normalization_R
velocity=states_normalized_out[:,3:]*ml_dsgp4.normalization_V

#let's plot it:
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(position[:,0], position[:,1], position[:,2])
ax.axis('equal');

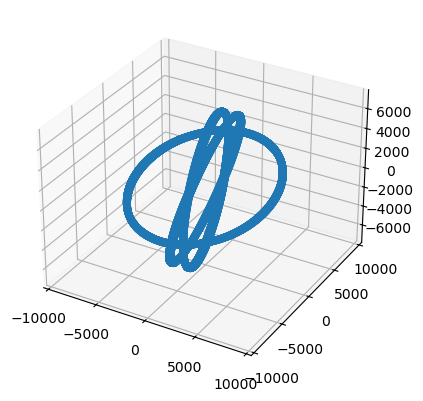
Single TLE Propagation with ML-dSGP4

#we use torch.no_grad() to avoid keeping track of the derivatives:
with torch.no_grad():    
    state_normalized_out=ml_dsgp4(tles_[0],tsinces)
state_normalized_out=state_normalized_out.detach().clone().numpy()

#if we want to unnormalize:
position=state_normalized_out[:,:3]*ml_dsgp4.normalization_R
velocity=state_normalized_out[:,3:]*ml_dsgp4.normalization_V

#let's plot it:
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(position[:,0], position[:,1], position[:,2])
ax.axis('equal');