Topology¶

The classes of this submodule are all instances of the same base class used to define the migration paths in the PyGMO.archipelago. When a new PyGMO.island is pushed back into the PyGMO.archipelago the various connections are rewired as to respect the topological properties defined by these classes.

The user will mainly use these classes in the following way:

from PyGMO import *
prob = problem.lennard_jones(5)
algo = algorithm.bee_colony(gen = 10) #instantiates artificial bee colony setting 10 generations for each algorithmic call
topo = topology.ring() #defines an empty ring topology
archi = archipelago(algo,prob,8,20,topology=topo) #connects 8 islands in a ring topology
archi.topology.draw() #requires networkx to be installed

Migration Probability¶

When defining the migration paths (edges of the DAG in the topology), one of the parameters is the migration probability, by default equal to 1. It is possible to change it globally for all edges:

from PyGMO import *
topo = topology.fully_connected(5) # Defines a 5-vertex ring topology
topo.set_weight(0.5)  # Changing the migration probability to 0.5 for all edges

specify a custom migration probability for all out-going edges of a node:

from PyGMO import *
topo = topology.fully_connected(3)  # Defines a 5-vertex ring topology
topo.set_weight(0.5)  # Change the migration probability to 0.5 for all edges
topo.set_weight(0, 0.1)  # Probability 0.1 for all out-going edges from island 0
topo.set_weight(2, 0.0)  # Probability 0.0 for all out-going edges from island 2 (effectively invalidating the migration path)

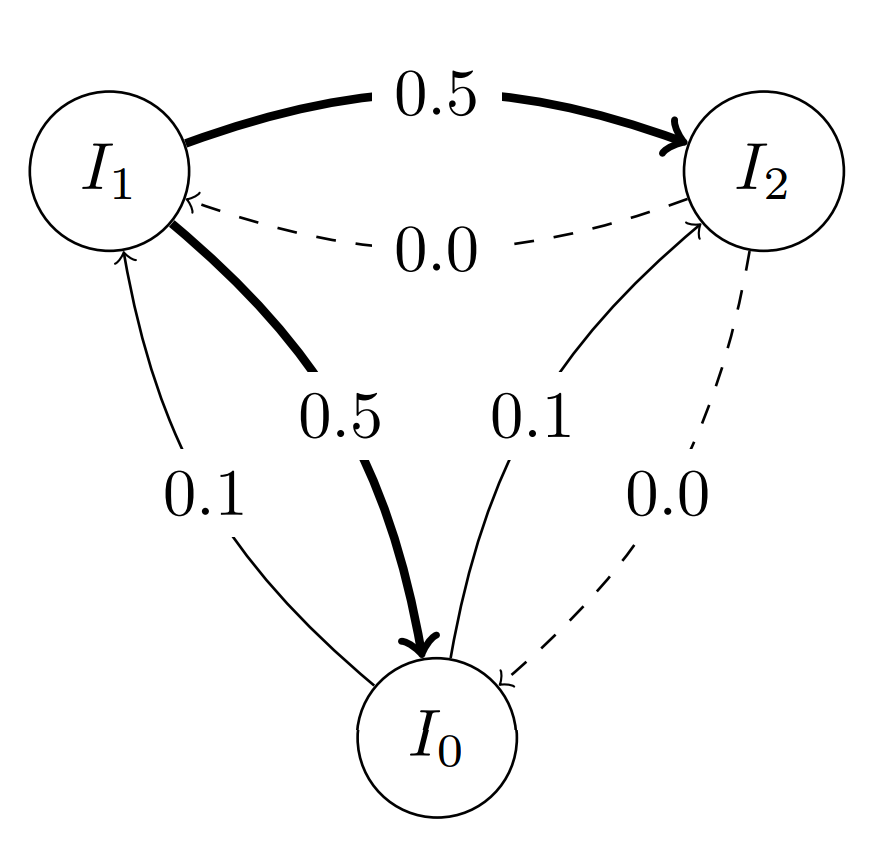
../_images/topo_prob_fully_connected.png

or specify a custom migration probability for individual edges:

from PyGMO import *
topo = topology.one_way_ring(5)  # Defines a 5-vertex ring topology
topo.set_weight(1, 2, 0.5)  # Changing the migration probability to 0.5 for edge 1 -> 2
topo.set_weight(2, 3, 0.2)  # Changing the migration probability to 0.2 for edge 2 -> 3
topo.set_weight(3, 4, 0.1)  # Changing the migration probability to 0.1 for edge 3 -> 4
topo.set_weight(4, 0, 0.05)  # Changing the migration probability to 0.05 for edge 4 -> 0

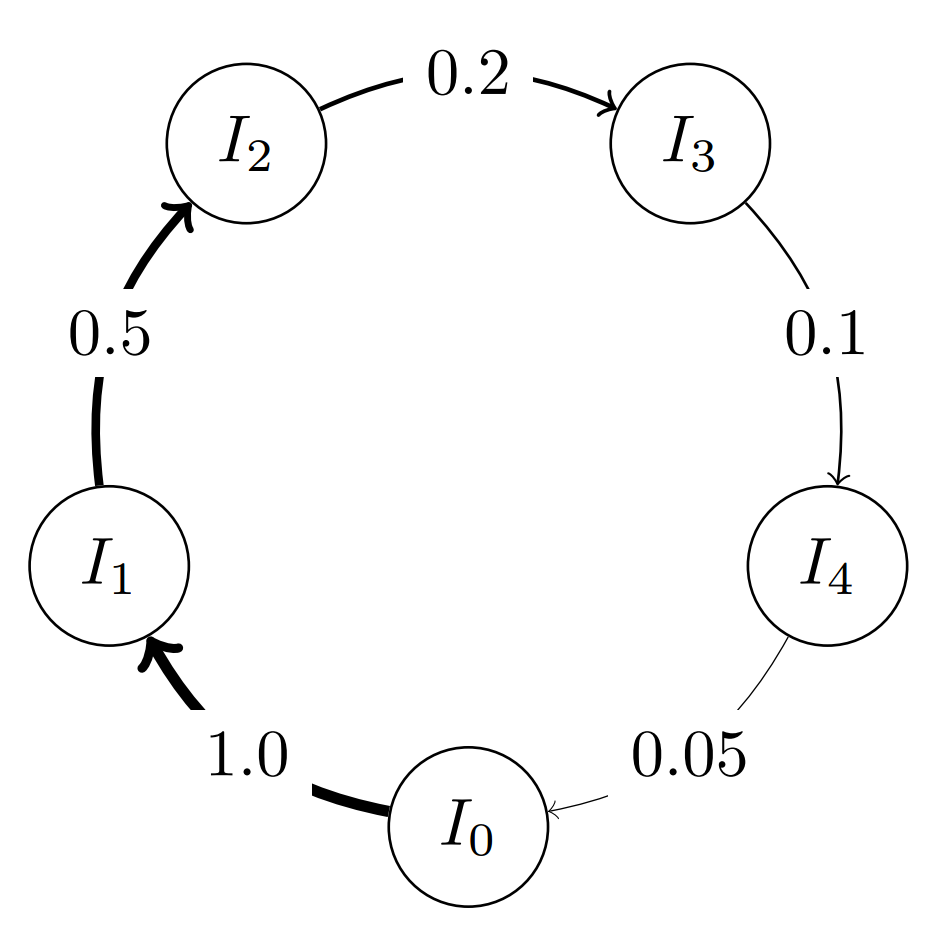
The Classes¶

class PyGMO.topology.base¶

Methods of the topology base class, shared by all topology objects.

set_weight((float)w)¶: Sets the weight for each edge in the topology.

set_weight((int)id, (float)w): Sets the weight for each edge outgoing from the vertex id

set_weight((int)id1, (int)id2, (float)w): Sets the weight for the edge between the vertices id1 and id2

class PyGMO.topology.unconnected¶

Unconnected topology (this corresponds to do parallel independent runs of the algorithms)

unconnected.__init__(nodes=0)¶

Constructs an unconnected topology

USAGE: topology.unconnected(nodes = 0)

nodes: number of nodes

unconnected.draw()¶

Draw topology using the draw() command from networkx.

USAGE: topology.draw(layout = “spring”, n_size = 15, scale_by_degree = False, n_color = ‘blue’, n_alpha = 0.5, e_alpha = 0.1, e_arrows=False)

layout: Network layout. Can be ‘spring’ or ‘circular’.
n_size: The size of nodes. Becomes scaling factor when scale_by_degree=True.
scale_by_degree: When True, nodes will be sized proportional to their degree.
n_color: Node color.
n_alpha: Transparency of nodes. Takes value between 0 and 1.
e_elpha: Transparency of edges. Takes value between 0 and 1.
e_arrows: Plots arrows on the edges for directed graphs
scale_by_degree: When True, nodes will be sized proportional to their degree.

The above image is produced by the code:

from PyGMO import *
topo = topology.unconnected(nodes=100)
topo.draw(layout='spring', n_size=15, e_arrows=False)

class PyGMO.topology.ring¶

Ring topology (links go in both directions)

ring.__init__(nodes=0)¶

Constructs a ring topology

USAGE: topology.ring(nodes = 0)

nodes: number of nodes

ring.draw()¶

Draw topology using the draw() command from networkx.

USAGE: topology.draw(layout = “spring”, n_size = 15, scale_by_degree = False, n_color = ‘blue’, n_alpha = 0.5, e_alpha = 0.1, e_arrows=False)

layout: Network layout. Can be ‘spring’ or ‘circular’.
n_size: The size of nodes. Becomes scaling factor when scale_by_degree=True.
scale_by_degree: When True, nodes will be sized proportional to their degree.
n_color: Node color.
n_alpha: Transparency of nodes. Takes value between 0 and 1.
e_elpha: Transparency of edges. Takes value between 0 and 1.
e_arrows: Plots arrows on the edges for directed graphs
scale_by_degree: When True, nodes will be sized proportional to their degree.

The above image is produced by the code:

from PyGMO import *
topo = topology.ring(nodes=30)
topo.draw(layout='circular', n_size=30, e_arrows=True, e_alpha=0.5)

class PyGMO.topology.one_way_ring¶

Ring topology (links go only in one direction)

one_way_ring.__init__(nodes=0)¶

Constructs a one_way_ring topology:

USAGE: topology.one_way_ring(nodes = 0)

nodes: number of nodes

one_way_ring.draw()¶

Draw topology using the draw() command from networkx.

USAGE: topology.draw(layout = “spring”, n_size = 15, scale_by_degree = False, n_color = ‘blue’, n_alpha = 0.5, e_alpha = 0.1, e_arrows=False)

layout: Network layout. Can be ‘spring’ or ‘circular’.
n_size: The size of nodes. Becomes scaling factor when scale_by_degree=True.
scale_by_degree: When True, nodes will be sized proportional to their degree.
n_color: Node color.
n_alpha: Transparency of nodes. Takes value between 0 and 1.
e_elpha: Transparency of edges. Takes value between 0 and 1.
e_arrows: Plots arrows on the edges for directed graphs
scale_by_degree: When True, nodes will be sized proportional to their degree.

The above image is produced by the code:

from PyGMO import *
topo = topology.one_way_ring(nodes=30)
topo.draw(layout='circular', n_size=30, e_arrows=True, e_alpha=0.5)

class PyGMO.topology.fully_connected¶

Fully connected topology (i.e. all islands are connected bi-directionally)

fully_connected.__init__(nodes=0)¶

Constructs a fully connected topology:

USAGE: topology.fully_connected(nodes = 0)

nodes: number of nodes

fully_connected.draw()¶

Draw topology using the draw() command from networkx.

USAGE: topology.draw(layout = “spring”, n_size = 15, scale_by_degree = False, n_color = ‘blue’, n_alpha = 0.5, e_alpha = 0.1, e_arrows=False)

layout: Network layout. Can be ‘spring’ or ‘circular’.
n_size: The size of nodes. Becomes scaling factor when scale_by_degree=True.
scale_by_degree: When True, nodes will be sized proportional to their degree.
n_color: Node color.
n_alpha: Transparency of nodes. Takes value between 0 and 1.
e_elpha: Transparency of edges. Takes value between 0 and 1.
e_arrows: Plots arrows on the edges for directed graphs
scale_by_degree: When True, nodes will be sized proportional to their degree.

The above image is produced by the code:

from PyGMO import *
topo = topology.fully_connected(nodes=30)
topo.draw(layout='circular', n_size=30, e_arrows=True, e_alpha=0.1)

class PyGMO.topology.pan¶

Islands are connected in a ring, except the island with id 0 that is connected to the ring only receiving migrants. This topology was first conceived to have global optimization happening on the outer ring while using a local optimizer in the island 0 to refine the solution (also seen as a memetic approach)

pan.__init__(nodes=0)¶

Constructs a pan topology: this is, essentially, a ring with a sink node. This topology was ‘invented’ to support a local optimization algorithm in the sink node

USAGE: topology.pan(nodes = 0)

nodes: number of nodes

pan.draw()¶

Draw topology using the draw() command from networkx.

USAGE: topology.draw(layout = “spring”, n_size = 15, scale_by_degree = False, n_color = ‘blue’, n_alpha = 0.5, e_alpha = 0.1, e_arrows=False)

layout: Network layout. Can be ‘spring’ or ‘circular’.
n_size: The size of nodes. Becomes scaling factor when scale_by_degree=True.
scale_by_degree: When True, nodes will be sized proportional to their degree.
n_color: Node color.
n_alpha: Transparency of nodes. Takes value between 0 and 1.
e_elpha: Transparency of edges. Takes value between 0 and 1.
e_arrows: Plots arrows on the edges for directed graphs
scale_by_degree: When True, nodes will be sized proportional to their degree.

from PyGMO import *
topo = topology.pan(nodes=10)
topo.draw(layout='spring', n_size=30, e_arrows = True)

class PyGMO.topology.rim¶

Islands are connected in a ring and they all are also connected to the No.0 island.

rim.__init__(nodes=0)¶

Constructs a rim topology: this is, essentially, a ring + one node that connects all ring nodes bi-directionally

USAGE: topology.rim(nodes = 0)

nodes: number of nodes

rim.draw()¶

Draw topology using the draw() command from networkx.

USAGE: topology.draw(layout = “spring”, n_size = 15, scale_by_degree = False, n_color = ‘blue’, n_alpha = 0.5, e_alpha = 0.1, e_arrows=False)

layout: Network layout. Can be ‘spring’ or ‘circular’.
n_size: The size of nodes. Becomes scaling factor when scale_by_degree=True.
scale_by_degree: When True, nodes will be sized proportional to their degree.
n_color: Node color.
n_alpha: Transparency of nodes. Takes value between 0 and 1.
e_elpha: Transparency of edges. Takes value between 0 and 1.
e_arrows: Plots arrows on the edges for directed graphs
scale_by_degree: When True, nodes will be sized proportional to their degree.

from PyGMO import *
topo = topology.rim(nodes=90)
topo.draw(layout='circular', n_size=30)

class PyGMO.topology.hypercube¶

Hypercube topology

hypercube.__init__(nodes=0)¶

Constructs a hypercube topology:

USAGE: topology.hypercube(nodes = 0)

nodes: number of nodes

hypercube.draw()¶

Draw topology using the draw() command from networkx.

USAGE: topology.draw(layout = “spring”, n_size = 15, scale_by_degree = False, n_color = ‘blue’, n_alpha = 0.5, e_alpha = 0.1, e_arrows=False)

layout: Network layout. Can be ‘spring’ or ‘circular’.
n_size: The size of nodes. Becomes scaling factor when scale_by_degree=True.
scale_by_degree: When True, nodes will be sized proportional to their degree.
n_color: Node color.
n_alpha: Transparency of nodes. Takes value between 0 and 1.
e_elpha: Transparency of edges. Takes value between 0 and 1.
e_arrows: Plots arrows on the edges for directed graphs
scale_by_degree: When True, nodes will be sized proportional to their degree.

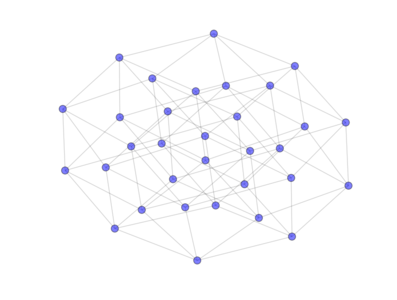
from PyGMO import *
topo = topology.hypercube(nodes=32)
topo.draw(layout='spring', n_size=90)

class PyGMO.topology.watts_strogatz¶

The Watts-Strogatz topology is a ring lattice network in which forward edges are rewired with random probability. Such a network has small-world properties, including short average path lengths and high clustering. When the push_back method is used all the connections are rewired (all links are bidirectional).

Watts-Strogatz topology in wikipedia

watts_strogatz.__init__(k=10, p=0.1, nodes=0)¶

Constructs Watts-Strogatz Topology:

USAGE: topology.watts-strogatz(k = 10, p = 0.1, nodes=0)

k: number of neighbours
p: rewiring probability [0,1]
nodes: number of nodes

watts_strogatz.draw()¶

Draw topology using the draw() command from networkx.

USAGE: topology.draw(layout = “spring”, n_size = 15, scale_by_degree = False, n_color = ‘blue’, n_alpha = 0.5, e_alpha = 0.1, e_arrows=False)

layout: Network layout. Can be ‘spring’ or ‘circular’.
n_size: The size of nodes. Becomes scaling factor when scale_by_degree=True.
scale_by_degree: When True, nodes will be sized proportional to their degree.
n_color: Node color.
n_alpha: Transparency of nodes. Takes value between 0 and 1.
e_elpha: Transparency of edges. Takes value between 0 and 1.
e_arrows: Plots arrows on the edges for directed graphs
scale_by_degree: When True, nodes will be sized proportional to their degree.

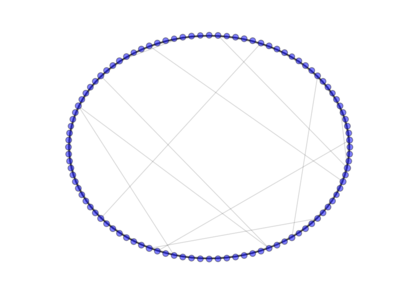
The above image is produced by the code:

from PyGMO import *
topo = topology.watts_strogatz(nodes=100, p=0.1)
topo.draw(layout='circular', n_size=3, scale_by_degree=True)

class PyGMO.topology.erdos_renyi¶

A random graph (all links are bidirectional)

erdos_renyi.__init__(p=0.1, nodes=0)¶

Constructs an Erdos-Renyi (random) topology:

USAGE: topology.erdos_renyi(p = 0.1, nodes=0)

p: wiring probability [0,1]
nodes: number of nodes

erdos_renyi.draw()¶

Draw topology using the draw() command from networkx.

USAGE: topology.draw(layout = “spring”, n_size = 15, scale_by_degree = False, n_color = ‘blue’, n_alpha = 0.5, e_alpha = 0.1, e_arrows=False)

layout: Network layout. Can be ‘spring’ or ‘circular’.
n_size: The size of nodes. Becomes scaling factor when scale_by_degree=True.
scale_by_degree: When True, nodes will be sized proportional to their degree.
n_color: Node color.
n_alpha: Transparency of nodes. Takes value between 0 and 1.
e_elpha: Transparency of edges. Takes value between 0 and 1.
e_arrows: Plots arrows on the edges for directed graphs
scale_by_degree: When True, nodes will be sized proportional to their degree.

The above image is produced by the code:

from PyGMO import *
topo = topology.erdos_renyi(nodes=100, p=0.03)
topo.draw(layout='spring', n_size=5, scale_by_degree=True)

class PyGMO.topology.barabasi_albert¶

Topology based on the Barabási-Albert (BA) model. (all links are bidirectional)

The network is grown in two phases:

The first m0 elements added to the network constitute a kernel of nodes connected to each other with high probability;

After the kernel is built, the next elements added to the network are connected randomly to m of the existing nodes; the probability of connection is biased linearly towards the most connected nodes.

barabasi_albert.__init__(m0=3, m=3, nodes=0)¶

Constructs an Barabasi-Albert topology:

USAGE: topology.barabasi_albert(m0 = 3, m = 3, nodes = 0)

m0: kernel size
m: number of random connections to be established when a new node is added.
nodes: number of nodes

barabasi_albert.draw()¶

Draw topology using the draw() command from networkx.

USAGE: topology.draw(layout = “spring”, n_size = 15, scale_by_degree = False, n_color = ‘blue’, n_alpha = 0.5, e_alpha = 0.1, e_arrows=False)

layout: Network layout. Can be ‘spring’ or ‘circular’.
n_size: The size of nodes. Becomes scaling factor when scale_by_degree=True.
scale_by_degree: When True, nodes will be sized proportional to their degree.
n_color: Node color.
n_alpha: Transparency of nodes. Takes value between 0 and 1.
e_elpha: Transparency of edges. Takes value between 0 and 1.
e_arrows: Plots arrows on the edges for directed graphs
scale_by_degree: When True, nodes will be sized proportional to their degree.

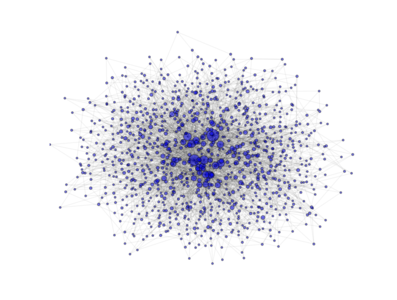
The above image is produced by the code:

from PyGMO import *
topo = topology.barabasi_albert(m0=3, m=3, nodes=1000)
topo.draw(layout='spring', n_size=1, scale_by_degree=True,e_alpha=0.03)

class PyGMO.topology.clustered_ba¶

Topology based on the Clustered Barabási-Albert (BA) model. (all links are bidirectional)

The network is grown in two phases:

The first m0 elements added to the network constitute a kernel of nodes connected to each other with high probability;

After the kernel is built, the next elements added to the network are connected randomly to m of the existing nodes; the probability of connection is biased linearly towards the most connected nodes. A link is established also between the m nodes with probability p

clustered_ba.__init__(m0=3, m=3, p=0.5, nodes=0)¶

Constructs a Clustered Barabasi-Albert topology:

USAGE: topology.clustered_ba(mm0 = 3, m=3, p=0.5, nodes = 0)

m0: kernel size
m: nnumber of random connections to be established when a new node is added
p: probability that a connection is established between two nodes that are adjacent to a new node
nodes: number of nodes

clustered_ba.draw()¶

Draw topology using the draw() command from networkx.

USAGE: topology.draw(layout = “spring”, n_size = 15, scale_by_degree = False, n_color = ‘blue’, n_alpha = 0.5, e_alpha = 0.1, e_arrows=False)

layout: Network layout. Can be ‘spring’ or ‘circular’.
n_size: The size of nodes. Becomes scaling factor when scale_by_degree=True.
scale_by_degree: When True, nodes will be sized proportional to their degree.
n_color: Node color.
n_alpha: Transparency of nodes. Takes value between 0 and 1.
e_elpha: Transparency of edges. Takes value between 0 and 1.
e_arrows: Plots arrows on the edges for directed graphs
scale_by_degree: When True, nodes will be sized proportional to their degree.

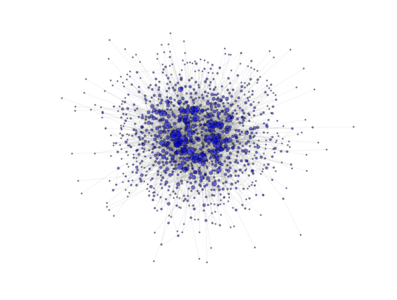
The above image is produced by the code:

from PyGMO import *
topo = topology.clustered_ba(m0=3, m=3, p=0.5,nodes=1000)
topo.draw(layout='spring', n_size=1, scale_by_degree=True,e_alpha=0.03)

class PyGMO.topology.ageing_clustered_ba¶

Topology based on the Ageing Clustered Barabási-Albert (BA) model. (all links are bidirectional)

The network is grown in two phases:

The first m0 elements added to the network constitute a kernel of nodes connected to each other with high probability;

After the kernel is built, the next elements added to the network are connected randomly to m of the existing nodes not older than a; the probability of connection is biased linearly towards the most connected nodes. A link is established also between the m nodes with probability p

ageing_clustered_ba.__init__(m0=3, m=3, p=0.5, a=1000, nodes=0)¶

Constructs a Clustered Barabási-Albert with Ageing vertices graph topology.:

USAGE: topology.clustered_ba(m0 = 3, m=3, p=0.5, a=1000, nodes = 0)

m0: kernel size
m: number of random connections to be established when a new node is added
p: probability that a connection is established between two nodes that are adjacent to a new node
a: ‘age’ at which a node ceases to make new connections.
nodes: number of nodes

ageing_clustered_ba.draw()¶

Draw topology using the draw() command from networkx.

USAGE: topology.draw(layout = “spring”, n_size = 15, scale_by_degree = False, n_color = ‘blue’, n_alpha = 0.5, e_alpha = 0.1, e_arrows=False)

layout: Network layout. Can be ‘spring’ or ‘circular’.
n_size: The size of nodes. Becomes scaling factor when scale_by_degree=True.
scale_by_degree: When True, nodes will be sized proportional to their degree.
n_color: Node color.
n_alpha: Transparency of nodes. Takes value between 0 and 1.
e_elpha: Transparency of edges. Takes value between 0 and 1.
e_arrows: Plots arrows on the edges for directed graphs
scale_by_degree: When True, nodes will be sized proportional to their degree.

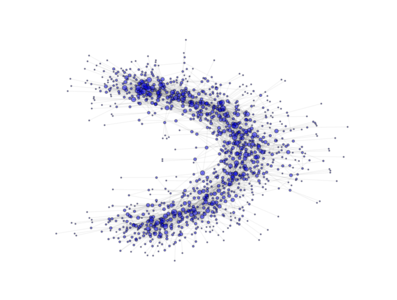
The above image is produced by the code:

from PyGMO import *
topo = topology.ageing_clustered_ba(m0=3, m=3, p=0.5,a=150,nodes=1000)
topo.draw(layout='spring', n_size=1, scale_by_degree=True,e_alpha=0.03)

class PyGMO.topology.custom¶

A custom topology. Allows for the construction of any topology via its unique methods.

push_back()¶: Adds a vertex

add_edge((int)id1, (int)id2, (float)w)¶: Adds a directed adge from vertex id1 to vertex id2, with an optional weight ‘w’ between id1 and id2 (by default 1.0)

remove_edge((int)id1, (int)id2)¶: Removes the directed adge from vertex id1 to vertex id2

remove_all_edges()¶: Removes all_edges

draw()¶: Uses Python networx module to draw the topology in a graphic window

Example:

from PyGMO import *
prob = problem.lennard_jones(5)
algo = algorithm.de(gen = 10)     #instantiates artificial bee colony with default params and 10 generations
topo = topology.custom()    #builds a custom topology
for i in range(30):
     topo.push_back()       #Now we have an unconnected topology of 30 vertices
topo.add_edge(1,2)
....
topo.add_edge(22,0)
archi = archipelago(algo,prob,30,20) #constructs an archipelago (we cannot assign here directly topo
                                     #to the kwarg topology as the archipelago constructor only takes empty topologies
archi.topology = topo                #sets the topology to the customly constructed one
archi.topology.draw()                #Draws the topology (this requires networkx to be installed)