Adding a new optimization problem

In this Tutorial we will learn how to code simple optimization problems (continuous, single objective, unconstrained), so that PyGMO can then apply all of its algorithmic power to solve it. In a nutshell, we will write a class deriving from PyGMO.problem.base and reimplement some of its ‘virtual’ methods.

Simple single objective problem

Let us start with defining one of the classic textbook examples of an optimization problem.

from PyGMO.problem import base

class my_problem(base):
    """
    De Jong (sphere) function implemented purely in Python.

    USAGE: my_problem(dim=10)

    * dim problem dimension
    """

    def __init__(self, dim=10):
        # First we call the constructor of the base class telling PyGMO
        # what kind of problem to expect ('dim' dimensions, 1 objective, 0 contraints etc.)
        super(my_problem,self).__init__(dim)

        # We set the problem bounds (in this case equal for all components)
        self.set_bounds(-5.12, 5.12)

    # Reimplement the virtual method that defines the objective function.
    def _objfun_impl(self, x):

        # Compute the sphere function
        f = sum([x[i] ** 2 for i in range(self.dimension)])

        # Note that we return a tuple with one element only. In PyGMO the objective functions
        # return tuples so that multi-objective optimization is also possible.
        return (f, )

    # Finally we also reimplement a virtual method that adds some output to the __repr__ method
    def human_readable_extra(self):
        return "\n\t Problem dimension: " + str(self.__dim)

Note that by default PyGMO will assume one wants to minimize the objective function. In the second part of this tutorial we will also see how it is possible to change this default behaviour.

To solve our problem we will use Artificial Bee Colony algorithm with 20 individuals.

from PyGMO import algorithm, island

prob = my_problem(dim=10)  # Create a 10-dimensional problem
algo = algorithm.bee_colony(gen=500)  # 500 generations of bee_colony algorithm
isl = island(algo, prob, 20)  # Instantiate population with 20 individuals
isl.evolve(1)  # Evolve the island once
isl.join()
print(isl.population.champion.f)

(5.800103096468531e-25,)

And we are done! Objective value in the order of \(10^{-25}\), no big deal for a sphere problem.

Maximization problem

Let’s consider now a maximization problem. To solve such a problem, two possibilities are available to the PaGMO/PyGMO user. The first one is to code the original problem as a minimization problem by premultiplying the objective function by \(-1\) (a technique wich is often used and requires no particular effort). If such a method is used, the final fitness value obtained with PyGMO has to be multiplied by \(-1\) to get back to the correct value.

A second method, more elegant and most of all serving the purpose to show the use of another virtual method which can be reimplemented in python objects deriving from base, is to override the function that compares two fitness vectors. This function is used by all pagmo algorithms to compare performances of individuals. By default, this function compares the fitness \(f_1\) to a fitness \(f_2\) and returns true if \(f_1\) dominates \(f_2\) (which is single objective optimization correspond to minimization). Let us see how...

class my_problem_max(base):
    """
    Analytical function to maximize.

    USAGE: my_problem_max()
    """

    def __init__(self):
        super(my_problem_max,self).__init__(2)
        self.set_bounds(-10, 10)

        # We provide a list of the best known solutions to the problem
        self.best_x = [[1.0, -1.0], ]

    # Reimplement the virtual method that defines the objective function
    def _objfun_impl(self, x):
        f = -(1.0 - x[0]) ** 2 - 100 * (-x[0] ** 2 - x[1]) ** 2 - 1.0
        return (f, )

    # Reimplement the virtual method that compares fitnesses
    def _compare_fitness_impl(self, f1, f2):
        return f1[0] > f2[0]

    # Add some output to __repr__
    def human_readable_extra(self):
        return "\n\tMaximization problem"

Additionally in the constructor we provide a list of all known global minima (we will use those later for testing). The list of corresponding objective function values will be then computed and accessible through best_f of the problem’s instance.

As before, we use our favorite optimization algorithm:

from math import sqrt

prob = my_problem_max()
algo = algorithm.de(gen=20)
isl = island(algo, prob, 20)
isl.evolve(10)
isl.join()

print("Best individual:")
print(isl.population.champion)

print("Comparison of the best found fitness with the best known fitness:")
for best_fitness in prob.best_f:
    print(best_fitness[0] - isl.population.champion.f[0])

print("L2 distance to the best decision vector:")
for best_decision in prob.best_x:
    l2_norm = 0
    for n in range(0, len(best_decision)):
        l2_norm +=  (best_decision[n] - isl.population.champion.x[n]) ** 2
    l2_norm = sqrt(l2_norm)
    print(l2_norm)

Best individual:
    Decision vector:        [1.0000035381312899, -1.000007979785372]
    Constraints vector:     []
    Fitness vector:         [-1.0000000000941514]

Comparison of the best found fitness with the best known fitness:
9.41513533803e-11
L2 distance to the best decision vector:
8.72899465051e-06

Note here that we used the best_f and best_x methods which return the best known fitness and decision vectors. The best_f vector is automatically available as we defined best_x in the problem. With these vectors, we can have an idea of the optimizer performances. The result of this optimization should be in order of \(10^{-11}\) for the comparison with the best fitness and \(10^{-6}\) for the distance to the best decision vector.

Multi-objective problem

As hinted before, users can also define their own multi-objective problem. In that case we need to overload the the base constructor with third argument stating the desired objective function dimension and return a tuple or a list with more than one element in the objective function implementation (both dimensions must agree).

class my_mo_problem(base):
    """
    A multi-objective problem.
    (This is actually a Python implementation of 2-dimensional ZDT-1 problem)

    USAGE: my_mo_problem()
    """

    def __init__(self, dim=2):
        # We call the base constructor as 'dim' dimensional problem, with 0 integer parts and 2 objectives.
        super(my_mo_problem,self).__init__(dim, 0, 2)
        self.set_bounds(0.0, 1.0)

    # Reimplement the virtual method that defines the objective function
    def _objfun_impl(self, x):
        f0 = x[0]
        g = 1.0 + 4.5 * x[1]
        f1 = g * (1.0 - sqrt(f0 / g))
        return (f0, f1, )

    # Add some output to __repr__
    def human_readable_extra(self):
        return "\n\tMulti-Objective problem"

We instantiate our problem as before, but this time we use one of the multi-objective algorithms available in PaGMO:

from PyGMO import population

prob = my_mo_problem()
algo = algorithm.sms_emoa(gen=2000)  # 2000 generations of SMS-EMOA should solve it
pop = population(prob, 30)
pop = algo.evolve(pop)

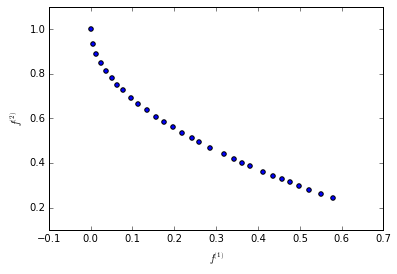
Since in the Multi-Objective world the idea of a single ‘champion’ solution is not very well defined, we plot the Pareto front of the whole population, i.e., the two objectives \(f_i^{(1)}\) and \(f_i^{(2)}\) of each individual \(i \in 1,\ldots,30\).

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

# Fold each objectives into vectors and print the Pareto front
F = np.array([ind.cur_f for ind in pop]).T
plt.scatter(F[0], F[1])
plt.xlabel("$f^{(1)}$")
plt.ylabel("$f^{(2)}$")
plt.show()

NOTE1: This problems of tutorial are implemented in PyGMO under the name PyGMO.problem.py_example and PyGMO.problem.py_example_max

NOTE2: When evolve is called from an island, the process is forked and transferred to another python or ipython instance. As a consequence, when writing your *obj*fun_impl you cannot use stuff like matplotlib to make interactive plots and alike. If you need, during development, to have this kind of support, use the algorithm evolve method (see the optimization of the Multi-Objective problemabove)

NOTE3: If performance is your goal, you should implement your problem in C++, and then expose it into Python.