Getting started with hypervolumes¶
This tutorial will cover the features introduced by the hypervolume functionality of PyGMO. First, we will describe how the user interface was designed and point out important notions that ought to be taken into account. Later, we will give several examples in order to get you started with the basic hypervolume computations.
Hypervolume interface and construction¶
The main class used for the computation of the hypervolume indicator (also known as Lebesgue Measure or S-Metric) and hypervolume contributions is the PyGMO.util.hypervolume class. You can import the hypervolume class using the following:
from PyGMO.util import hypervolume
'hypervolume' in dir() # Returns True
Since the computation of the hypervolume indicator and the hypervolume contributions are bound tightly to multi-objective optimization, we provide two ways of constructing a hypervolume object. The first one uses the fitness values of the individuals of a population for the input point set:
from PyGMO import *
from PyGMO.util import *
prob = problem.dtlz(prob_id = 2, k = 10, fdim = 3) # Construct DTLZ-2 problem with 3-dimensional fitness space
pop = population(prob, 50) # Construct the population object
hv = hypervolume(pop) # Construct the hypervolume object from the population object
Note
You need to reconstruct the hypervolume object if the fitness values of the population are changing. The point set which is saved in the hypervolume object is not updated automatically.
The second way of construction uses an explicit representation of coordinates for the input point set:
from PyGMO.util import *
hv = hypervolume([[1,0],[0.5,0.5],[0,1]])
This type of construction is especially useful when you have an explicit geometry you want to analyze rather than implicit coordinates by the fitness values of a population that rely on the objective function of the corresponding problem.
Computing the hypervolume indicator and hypervolume contributions¶
Before we give an overview of each hypervolume feature, let us discuss the assumptions we make regarding the reference point and the input set of points to be valid:
- We assume minimization in every dimension, that is, a reference point is required to be numerically larger or equal in each objective, and strictly larger in at least one of them.
- Although the hypervolume for one dimension is well defined mathematically, we require any input data to have a matching dimension of at least 2, including the reference point.
PyGMO helps you with these assumptions as it performs checks upon construction and also before each computation and will give you an error if your input set or your reference point does not fulfill these criteria. This check can be turned off using
hv = hypervolume([ (1,0), (0.5,0.5), (0,1) ], verify=False)
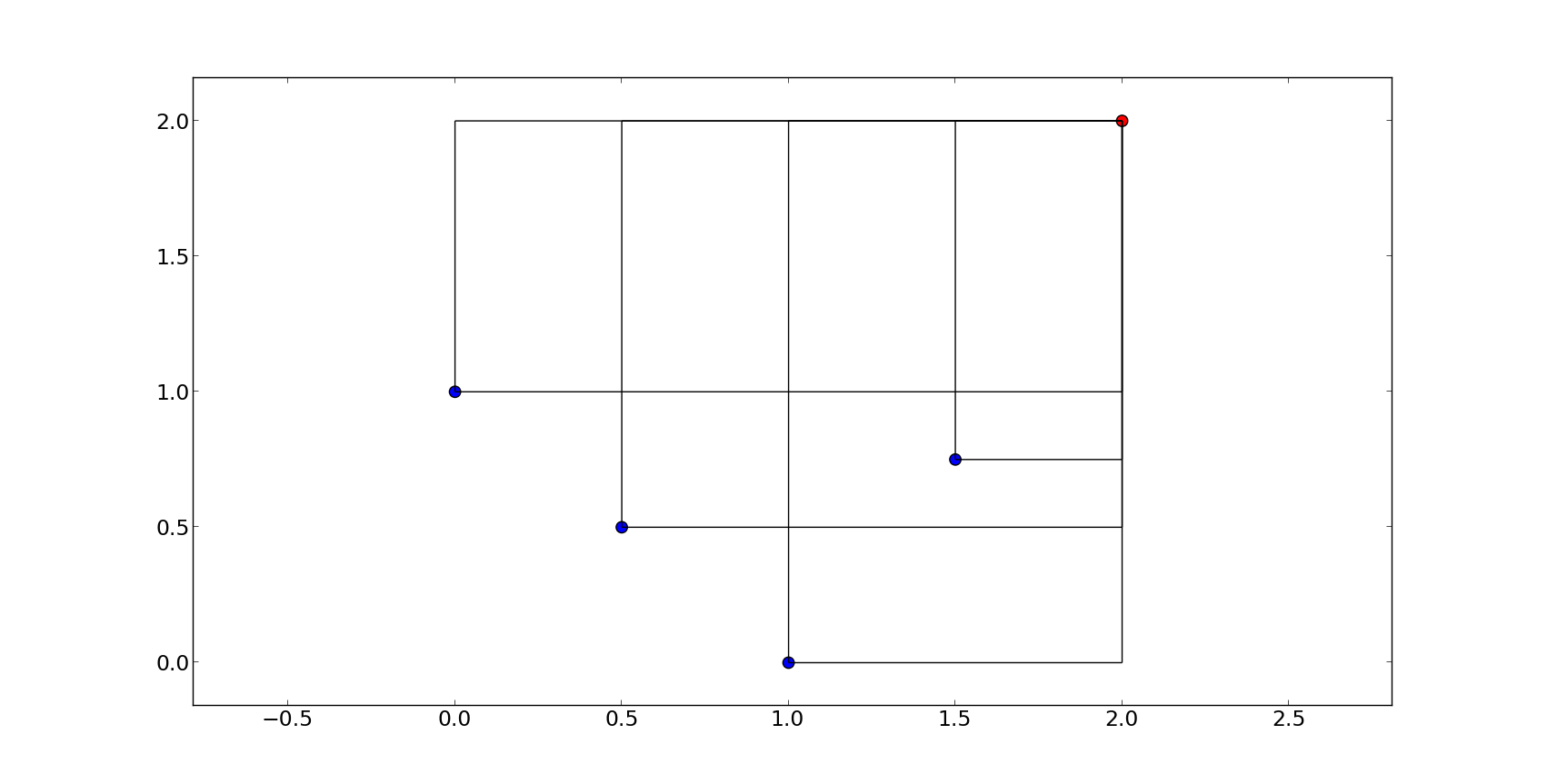
For simplicity, we will use this simple 2-dimensional front as an example to show you the basic features of a hypervolume object:
from PyGMO.util import *
hv = hypervolume( ((1, 0), (0.5, 0.5), (0, 1), (1.5, 0.75)) )
ref_point = (2,2)
hv.compute(r=ref_point) # Returns 3.25 as an answer
We will refer to each point by it’s position on the x-axis, e.g. first point is the point (0,1), fourth point is (1.5, 0.75) etc. The plot below shows you the overall geometry of the example with the reference point painted red.
Once the hypervolume object is created, it allows for the computation of the following figures:
- compute - Returns the joint hypervolume of the set of points (S-Metric).
# hv and ref_point refer to the data above
hv.compute(r=ref_point) # Returns 3.25 as an answer
- exclusive - Returns the exclusive hypervolume by the point at given index. The exclusive hypervolume is defined as the part of the space dominated exclusively by one point and is also called its (hypervolume) contribution.
# hv and ref_point refer to the data above
hv.exclusive(1, r=ref_point) # Returns 0.25 as an answer
hv.exclusive(3, r=ref_point) # Returns 0.0 as an answer since point at index 3 (fourth from the left) is dominated
- least_contributor - Returns the index of a point contributing the least to the hypervolume.
# hv and ref_point refer to the data above
hv.least_contributor(r=ref_point) # Returns 3 as an answer, since point at that index contributes no hypervolume
- greatest_contributor - Returns the index of a point contributing the most to the hypervolume.
# hv and ref_point refer to the data above
hv.greatest_contributor(r=ref_point) # Returns either 0 or 2 as an answer
Note
In case of several least/greatest contributors, PyGMO returns only one contributor out of all candidates arbitrarily.
- contributions - Returns a list of contributions for all points in the set. This returns the same results as the successive call to the exclusive method for each of the points. Due to the implementation, calling contributions once can be much faster (up to a linear factor) than computing all contributions separately by using exclusive.
# hv and ref_point refer to the data above
hv.contributions(r=ref_point) # Returns a tuple (0.5, 0.25, 0.5, 0.0)
Since all of the methods above require a reference point, it is often useful to generate one automatically:
- get_nadir_point - Generates a point that is “worse” than any other point in each of the objectives. By default, it generates a point whose objectives are maximal among each objective for the whole point set, called the nadir point. Additionally, it is possible to provide an offset which is added to each coordinate of the nadir point. Doing so is recommended since any point sharing the “worst” value for a given objective with the reference point will contribute zero to the overall hypervolume otherwise.
This following short script presents all features mentioned above:
from PyGMO import *
from PyGMO.util import *
# Initiate a 4-objective problem
# and a population of 100 individuals
prob = problem.dtlz(prob_id=4, k = 12, fdim=4)
pop = population(prob, 100)
# Construct the hypervolume object
# and get the reference point off-setted by 10 in each objective
hv = hypervolume(pop)
ref_point = hv.get_nadir_point(10)
print hv.compute(ref_point)
print hv.exclusive(0, ref_point)
print hv.least_contributor(ref_point)
print hv.greatest_contributor(ref_point)
print hv.contributions(ref_point)
# Evolve the population some generations
algo = algorithm.sms_emoa(gen=2000)
pop = algo.evolve(pop)
# Compute the hypervolume indicator again.
# This time we expect a higher value as SMS-EMOA evolves the population
# by trying to maximize the hypervolume indicator.
hv = hypervolume(pop)
print hv.compute(ref_point)