Racing the individuals in stochastic optimization problems

Background

When trying to solve a stochastic optimization problem, an algorithm will have to handle the stochasticity in order to obtain the true optimal solution. During the optimization process of a population based algorithm, it is often required to identify which individuals are more superior than the others, for example in the environmental selection process of SGA, neighbourhood information update of PSO, and so on. In this tutorial we will introduce the method of racing which tries to achieve the task efficiently. Our main goal is to reconstruct the full ordering among the individuals by their true performance. The main obstacle is that we can only observe the non-determinstic performance of each individual, whose ground truth is distorted by the stochasticity of the problem. A direct consequence of this goal is the ability to extract N top performing individuals among a pool of them, which can be a very useful information for an optimization algorithm.

Racing with PyGMO

Racing is a mechanism based on statistical testing, and the main idea is that an individual can be dropped immediately once statistical significance evidence is present, so that we do not waste unnecessary objective function evaluation on these clearly inferior individuals. This way, the other individuals whose performance are not obviously good or bad will be evaluated more frequently – possibly yielding a better accuracy. The current racing implementation is based on F-Race [1], and some implementation details are adapted from [2].

In this tutorial we will look at a special class of stochastic problems – the noisy problems. We will use Ackley as the base (noise-less) problem. To race the individuals in the population, we can simply do:

In [1]: from PyGMO import *
In [2]: prob = problem.noisy(problem.ackley())
In [3]: pop = population(prob, 10)
In [4]: winners = pop.race(1)

which will extract a single winner. There are some other parameters which can be adjusted, for example:

In [5]: winners = pop.race(3, 10, 200, 0.01)

will race until 3 individuals remain, evaluate at the start every individuals for at least 10 times, with an objective function evaluation budget of 200 times and perform statistical testing at the confidence level of 0.01. You can even provide a list of indices to specify a subset of individuals to be raced, for example:

In [6]: winners = pop.race(1, 10, 200, 0.01, [0,1,2,3,4])

will return the best individual among the first five individuals in the population.

Why racing: A comparative study

Racing does not magically identify the winners – it still requires that additional function evaluation be performed. One may ask: why should one use racing, when there is a simpler approach of simply evaluating each individual multiple times equally? In the following we try to answer this question by justiying the use of racing.

Assume that we have a limited amount of objective evaluation budget, and that we want to extract the best few individuals from a population. The following are the possible approaches that we could use:

• Brute-force by fitness: Evaluate all individuals an equal number of times and record the average of their fitness values. Identify the best few individuals using the sorted averaged fitness values. Note that this method is only applicable for use in unconstrained, single-objective problems.
• Brute-force by ranks: Similar to the above, but replace the raw fitness values to a nominal relative ranking. This can be done by using the built-in get_best_idx() function in population class. This method is thus able to handle constrained or multi-objective problems.
• Racing: This is similar to the brute-force by ranks method, except that the computational budget for function evaluation is more cleverly distributed among different individuals.

To quantitatively measure the peformance of each method, we define a notion called rank sum error. Rank sum error measures how well a method extracts the true winners.

To obtain the rank sum error metric, we first construct population on the basic noise-less problem and calculate the original ordering of the individuals (for example, via get_best_idx()). Then, we construct another population (on which the racing / brute-force method will be executed) associated with the corresponding noisy problem, by inserting the individuals using the ordering calculated previously. This way, although the fitness of the individuals are disguised by the noise, we know that the best individual is at index 0, the second best is at index 1, and so on. As our goal is to extract the best individuals, the ground truth rank sum is simply the sum of [0,1,2,3,...,pop_size]. We compute the rank sum of the winnner list returned by different methods, and denote its differerence with the ground truth as the rank sum error.

We set up a few configurations and plot the rank sum errors for different methods, averaged over 200 independent trials. The default strength of the noise is normally distributed, having a zero mean and a standard deviation of 0.5. Please refer to racing.py contained in PyGMO examples/ directory for more details.

Varying noise level

Problems considered: Ackley (Single objective), CEC2006-g1 (Constrained single objective), ZDT1 (Multi-objective)

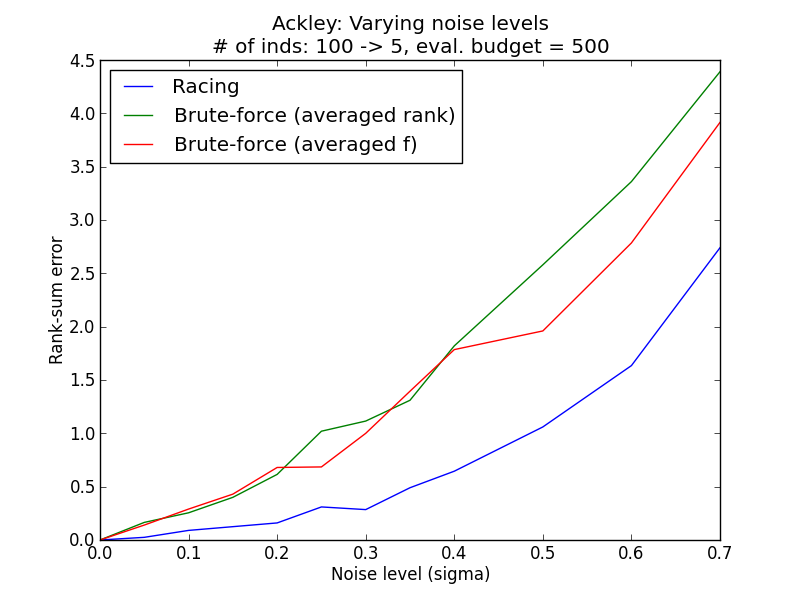
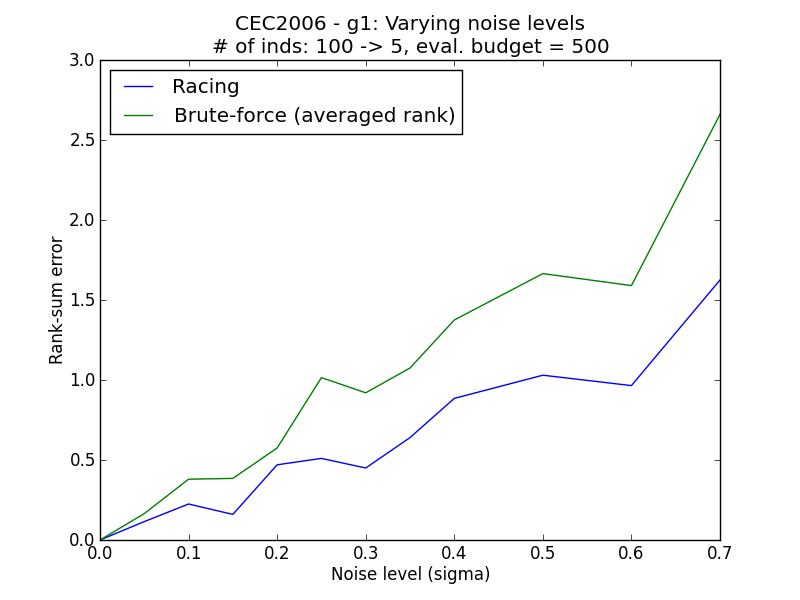
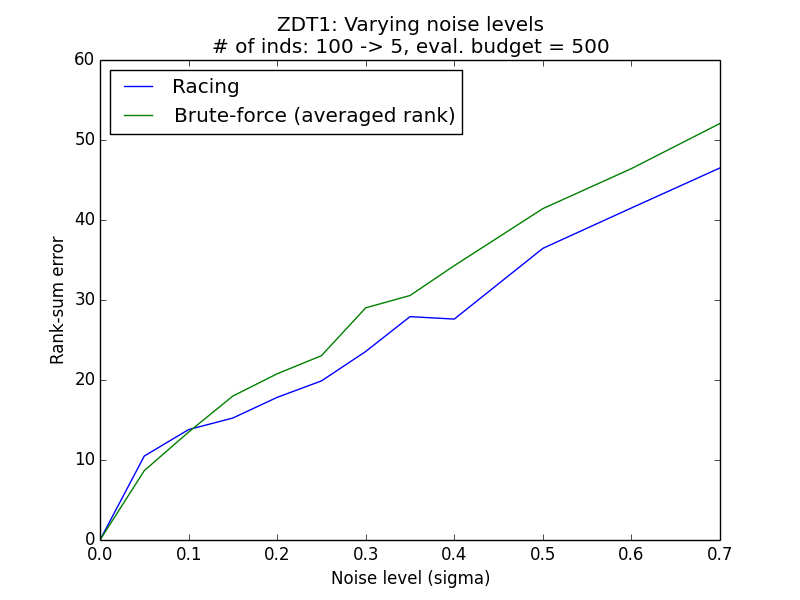
Varying initial population sizes

Problems considered: Ackley (Single objective), CEC2006-g1 (Constrained single objective), ZDT1 (Multi-objective)

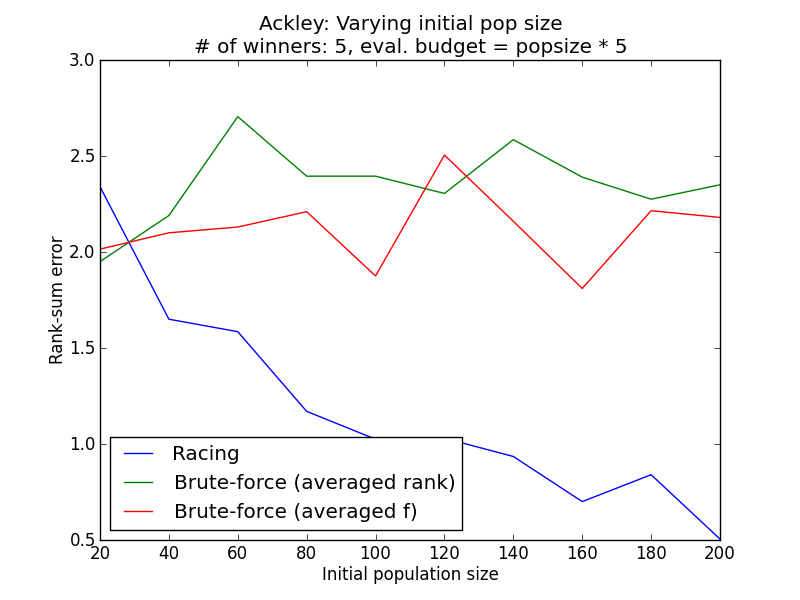
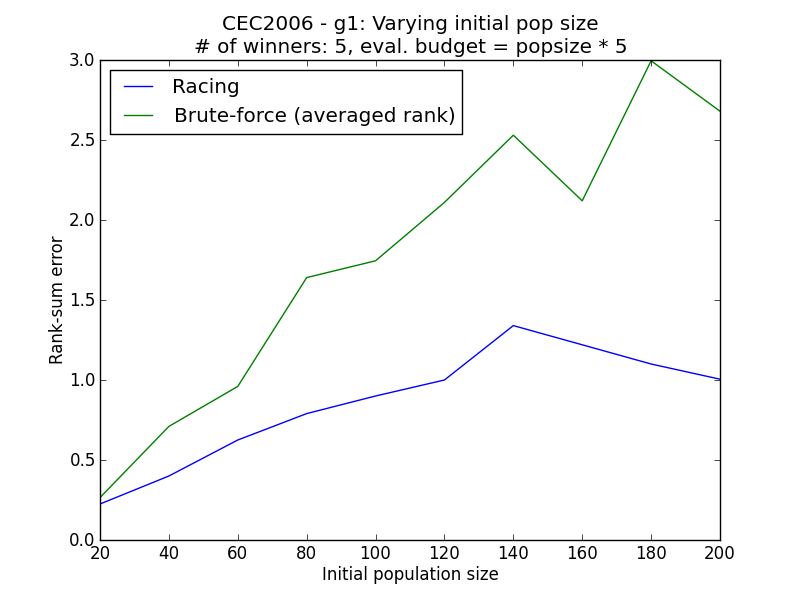
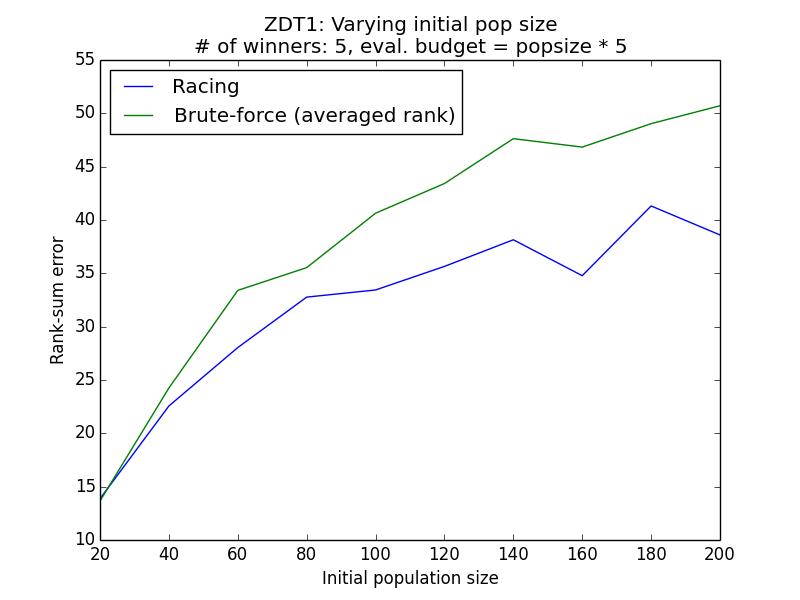
Varying evaluation budget

Problems considered: Ackley (Single objective), CEC2006-g1 (Constrained single objective), ZDT1 (Multi-objective)

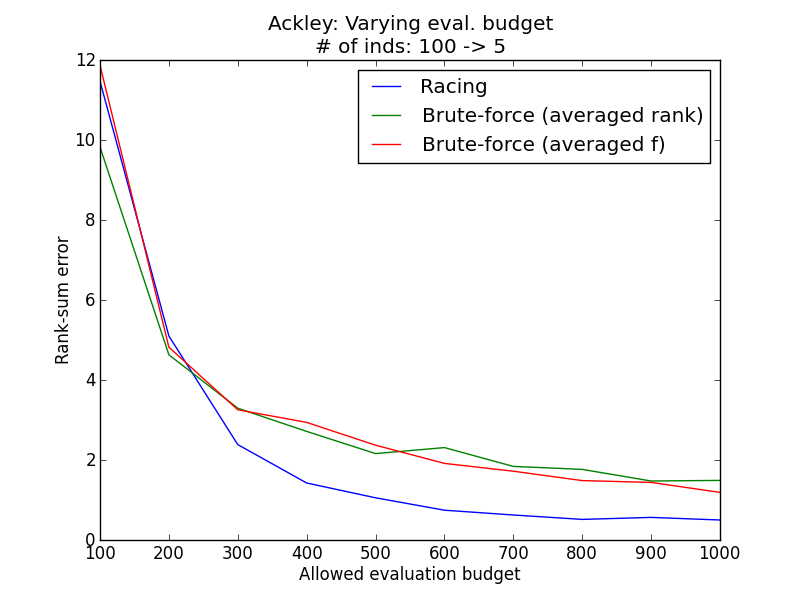
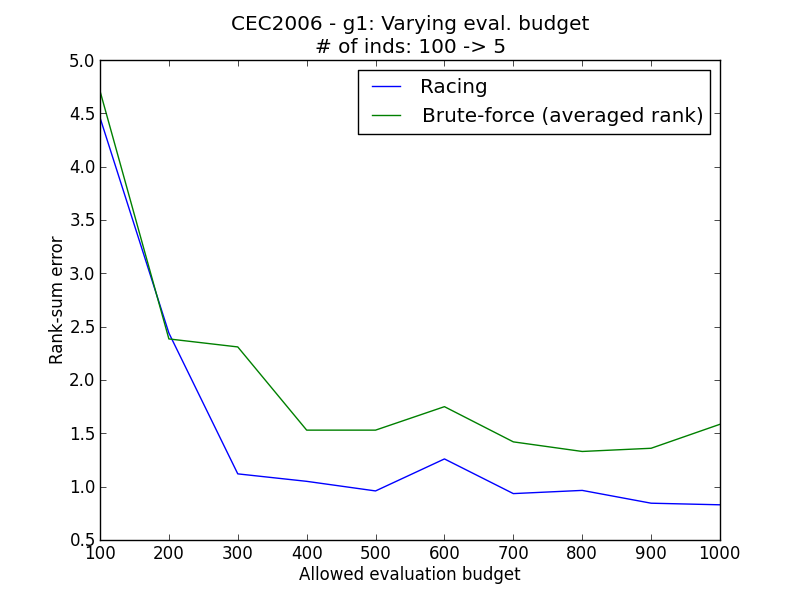
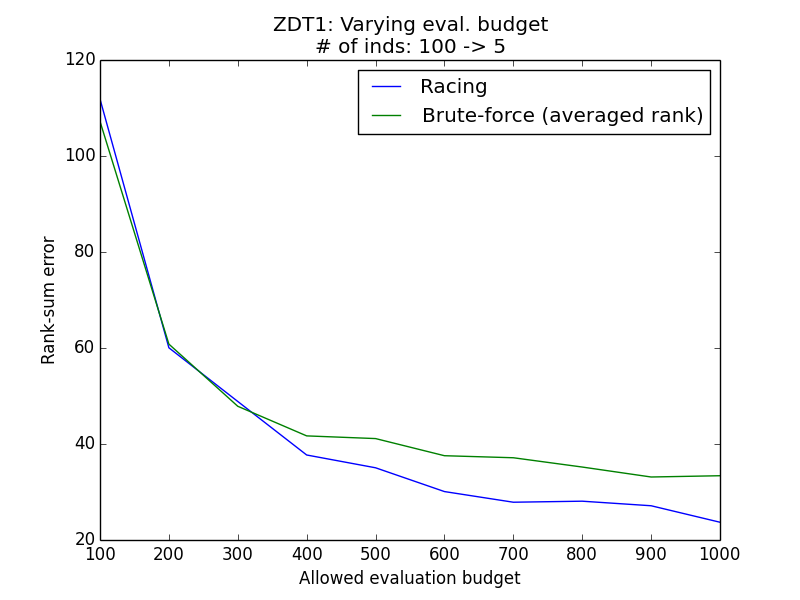
Generally, it is observed that the racing method yields lower rank sum error than the simple methods. The simulation results above demonstrate empirically how racing could improve the ability to reconstruct the correct ordering of the individuals in face of a stochastic environment.

Note

For multiobjective case the benefit of racing is more apparent when budget is large enough. Brute force can even be as good as racing when noise is high or initial population size is large. A possible reason is due to the involvement of Pareto ranks in racing, which brings about large “jumps” in the observation data, causing difficulties for the statistical testing. One possible way to reduce this effect is to use a larger budget. This implies that while racing is able to handle multiobjective problems, they require a more careful treatment.

[1]	Birattari, M., Stützle, T., Paquete, L., & Varrentrapp, K. (2002). A Racing Algorithm for Configuring Metaheuristics. GECCO ’02 Proceedings of the Genetic and Evolutionary Computation Conference (pp. 11–18). Morgan Kaufmann Publishers Inc.

[2]	Heidrich-Meisner, Verena, & Christian Igel (2009). Hoeffding and Bernstein Races for Selecting Policies in Evolutionary Direct Policy Search. Proceedings of the 26th Annual International Conference on Machine Learning, pp. 401-408. ACM Press.