Using hypervolumes in your own algorithm¶

In this tutorial we will show how to use the hypervolume features in your own custom evolutionary algorithms. If you haven’t already, we suggest getting familiar with the tutorial Adding a new algorithm.

As it is often the case in the tutorials, we will present a fairly simple MOO algorithm, which we would not expect to be particularly good.

from PyGMO import *
from PyGMO.util import *
import random

class my_hv_moo_alg(algorithm.base):
   """
   A custom steady-state algorithm, based on the hypervolume computation.
   """

   def __init__(self, gen = 10, p_m = 0.02):
      """
      Constructs an instance of the algorithm.

      USAGE: my_hv_moo_alg(gen=10, p_m=0.02)

      NOTE: Evolves the population using the least contributor feature.

      * gen: number of generations
      * p_m: probability of mutation
      """
      # We start by calling the base constructor
      super(my_hv_moo_alg,self).__init__()
      # Store the number of generations
      self.__gen = gen
      self.__p_m = p_m

   # Performs a very simple crossover step
   def cross(self, ind1, ind2):
      x1 = ind1.cur_x
      x2 = ind2.cur_x
      return tuple(random.choice((x1[i], x2[i],)) for i in xrange(len(x1)))

   # Gaussian mutation
   def mutate(self, x, lb, ub):

      # Implementation of the Gaussian operator
      def _g_op(i):
         return min(max(random.gauss(x[i], (ub[i]-lb[i]) * 0.1), lb[i]), ub[i])

      # Condition for the mutation to happen
      def _rnd_mut():
         return random.random() < self.__p_m

      return tuple(_g_op(i) if _rnd_mut() else x[i] for i in xrange(len(x)))

   # Evolve method
   def evolve(self, pop):
      #If the population is empty (i.e. no individuals) nothing happens
      if len(pop) == 0:
           return pop

      #The algorithm now starts manipulating the population
      prob = pop.problem
      lb, ub = prob.lb, prob.ub
      for s in range(self.__gen):
         # Initiate new individual by a crossover of two random individuals
         idx1 = random.randint(0, len(pop) - 1)
         idx2 = (idx1 + random.randint(0, len(pop) - 2)) % len(pop)
         ind1 = pop[idx1]
         ind2 = pop[idx2]

         new_x = self.mutate(self.cross(ind1, ind2), lb, ub)
         pop.push_back(new_x)

         # Remove the least contributor
         hv = hypervolume(pop)
         ref_point = hv.get_nadir_point(1.0)
         lc_idx = hv.least_contributor(ref_point)

         pop.erase(lc_idx)
      return pop

   def get_name(self):
         return "Custom HV-based MOO"

def main():
   prob = problem.dtlz(2)
   alg = my_hv_moo_alg(gen = 100, p_m=0.02)
   pop = population(prob, 100)
   # Establish a constant reference point, so the increase is noticed
   ref_point = (3000,) * 3
   for _ in xrange(100):
      pop = alg.evolve(pop)
      print "P-Distance: %.5f, Hypervolume: %.5f" % (prob.p_distance(pop), hypervolume(pop).compute(ref_point))
   prob.plot(pop)

if __name__ == "__main__":
   main()

You can copy the whole code above and save it as a python script (e.g. my_alg.py), this way you can execute it yourself by issuing the following in the command line: python my_alg.py.

The algorithm does the following in the evolve method:

Establish a new individual by performing a very simple crossover on two random individuals
Apply the Gaussian mutation operator
Push the newly obtained vector to the population
Establish the least contributor using the PyGMO.util.hypervolume object
Remove the least contributor from the population

Script above should produce an output similar to the one below:

P-Distance: 0.77281, Hypervolume: 26999518559.47130
P-Distance: 0.66491, Hypervolume: 26999704053.34119
P-Distance: 0.51330, Hypervolume: 26999704183.90998
.
.
.
P-Distance: 0.00026, Hypervolume: 26999999999.42529
P-Distance: 0.00026, Hypervolume: 26999999999.42529
P-Distance: 0.00024, Hypervolume: 26999999999.42531

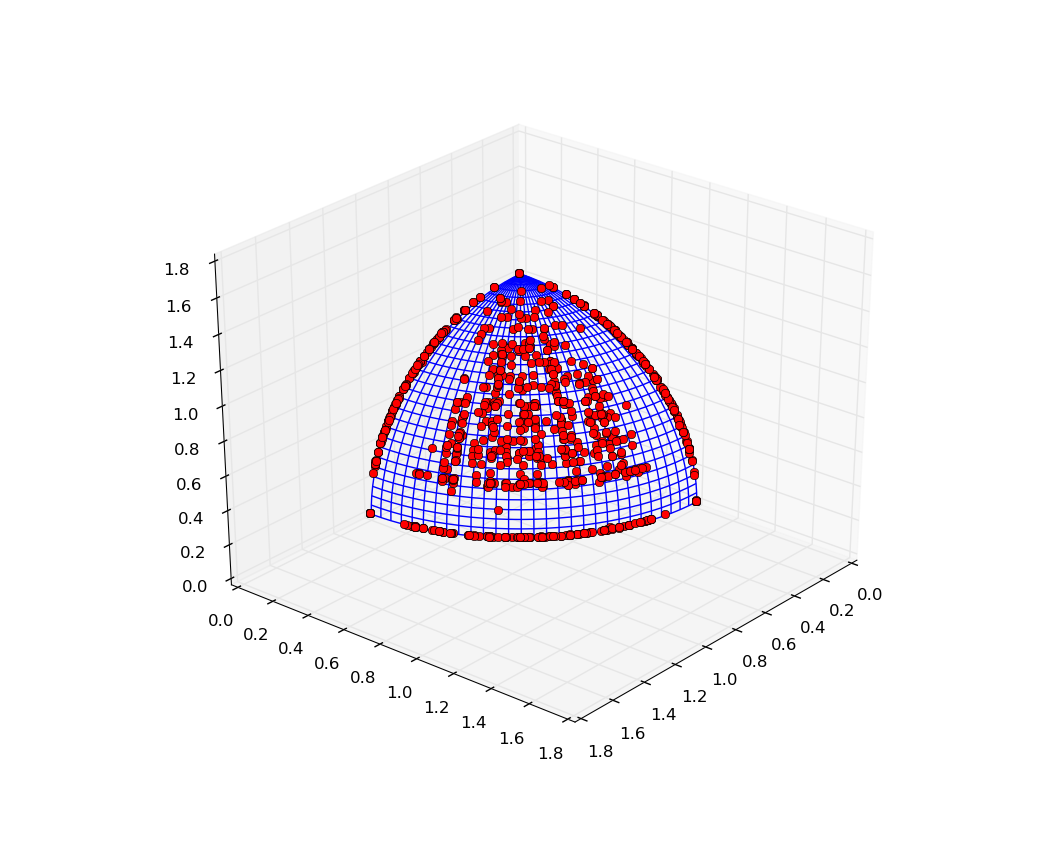
We can observe an improvement over the consecutive generations both in the distance to the Pareto front (P-Distance) and the hypervolume indicator itself. The result of the script should be a plot similar to the one below:

Custom algorithms can also be used in the archipelago evolution. For this, we will employ the information from the previous tutorial Migration based on hypervolume contribution. Substitute the main() method in the script above with the following experiment, which will initiate an archipelago with our custom algorithm on-board.

def main():
   prob = problem.dtlz(2)
   alg = my_hv_moo_alg(gen = 100, p_m=0.02)

   # Initiate the migration policies
   s_pol = migration.hv_best_s_policy(0.1, migration.rate_type.fractional)
   r_pol = migration.hv_fair_r_policy(0.1, migration.rate_type.fractional)

   # Set up the archipelago
   n_islands = 16
   n_individuals = 64
   arch = archipelago(topology=topology.fully_connected())
   islands = [island(alg, prob, n_individuals, s_policy=s_pol, r_policy=r_pol) for i in xrange(n_islands)]
   for i in islands:
      arch.push_back(i)

   # Evolve
   n_steps = 20
   for s in xrange(n_steps):
      print "Evolving archipelago, step %d/%d" % (s, n_steps)
      arch.evolve(1)

   # Merge all populations across the islands together
   pop = population(prob)
   for isl in arch:
      for ind in isl.population:
         pop.push_back(ind.cur_x)

   print "Final P-Distance: ", prob.p_distance(pop)
   prob.plot(pop)

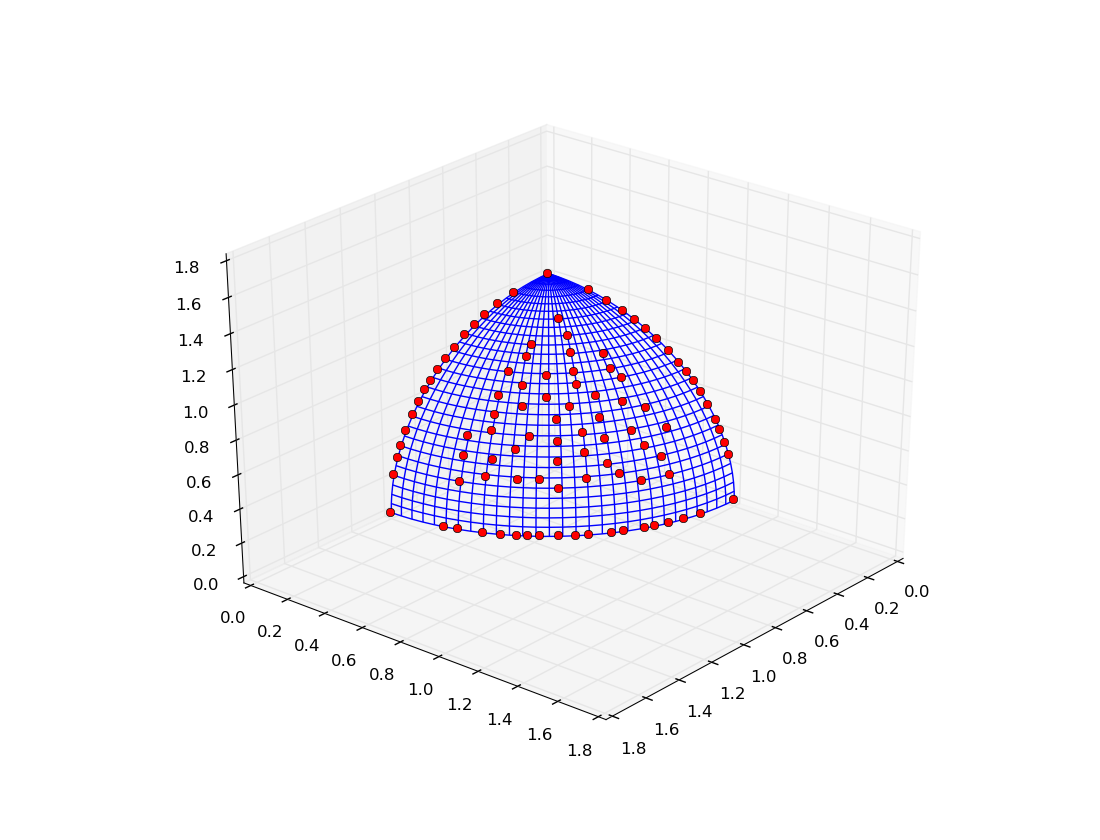
The execution of the script should result in a plot similar to the one below: