Basic Multi-Objective Functionalities

In this tutorial we will learn how to use PyGMO to solve multiple-objective optimization problems. In essence we will learn how to use the methods that deal with Pareto-optimality, in particular those of the class population

This tutorial assumes an ipython interactive environment. Let us start to define our population:

In [1]: from PyGMO import *
In [2]: prob = problem.zdt(1)
In [3]: pop = population(prob,10)

We here make use of first problem of the ZDT benchmark suite and we created a population containing 10 individuals randomly created within the box bounds. Which individuals belong to which preto front? We can immediately see this by typing:

In [4]: pop.compute_pareto_fronts()
Out[4]: ((0, 1, 6), (2, 5, 7), (4,), (8, 9), (3,))

For larger populations, a good visualization of the different Pareto Fronts can be obtained:

In [5]: pop = population(prob,100)
In [6]: pop.plot_pareto_fronts()

which will produce a plot similar to:

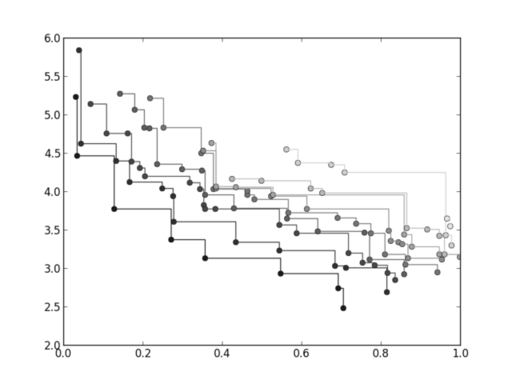
where each successive pareto front is plotted in darker colour. If we now type:

In [7]: algo = algorithm.nsga_II(gen = 250)
In [8]: pop = algo.evolve(pop)
In [9]: pop.plot_pareto_fronts()

we have instantiated the algorithm Non-dominated Sorting Genetic Algorithm, able to tackle multi-objective problems, defining the number of generations to 250. In the next line use directly the method evolve of the algorithm to evolve the population. We could have also, similarly, defined an island and use the evolve method of the island:

In [7]: algo = algorithm.nsga_II(gen = 250)
In [8]: isl = island(algo,pop)
In [9]: isl.evolve(1)
In [10]: isl.population.plot_pareto_fronts()

This block of code is equivalent to the previous one showing how, in PyGMO, islands are not necessary to run algorithms in single threads. They only become really necessary in connection to archipelago evolutions. In any case at the end of our evolution we may plot again the pareto front:

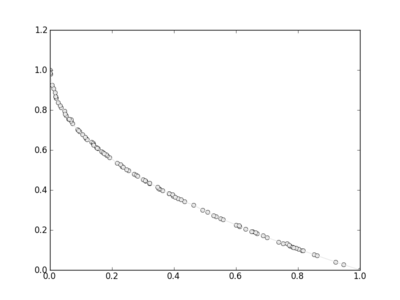
In [10]: pop.plot_pareto_fronts()

to finally have: