The Noisy meta-problem

The noisy meta-problem introduces noise into regular PyGMO problem, rendering them stochastic. More specifically, the observed fitness and constraint vectors from such problems have been corrupted by noises. Currently, two types of noise distributions are supported, namely the normal distribution and uniform distribution.

from PyGMO import *
prob = problem.ackley(1)
prob_noisy_normal = problem.noisy(prob, trials=1, param_first=0.0, param_second=0.1, noise_type=problem.noisy.noise_distribution.NORMAL)
prob_noisy_uniform = problem.noisy(prob, trials=1, param_first=-3, param_second=3, noise_type=problem.noisy_noise_distribution.UNIFORM)

The construction parameters control the following aspects of the noisy transform:

• Noise distribution: The Gaussian noise is characterized by a mean of param_first and a standard deviation of param_second, while the uniformly noise is uniformly distributed between param_first and param_second.
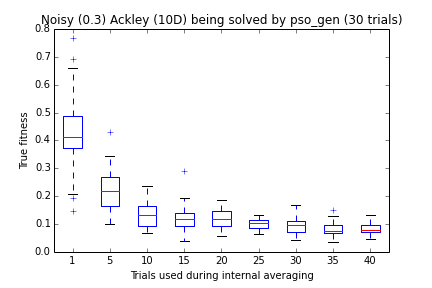
• Internal averaging: The noisy meta-problem provides an internal mechanism to perform averaging via repeated evaluation before reporting the fitness / constraint vectors, at the expense of increase computational budget. The number of samples to average over is controlled by the parameter trials.

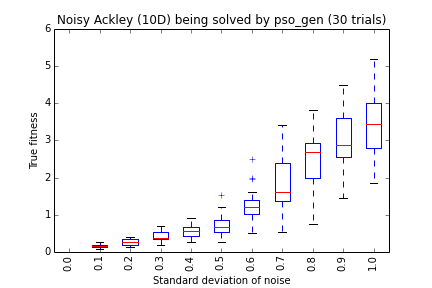
The fitness landscape (or more precisely the distribution of fitness values at each decision value) of a noisy one-dimensional Ackley problem is visualized in the following figures. The solid line is the fitness in case of a noise-less problem.

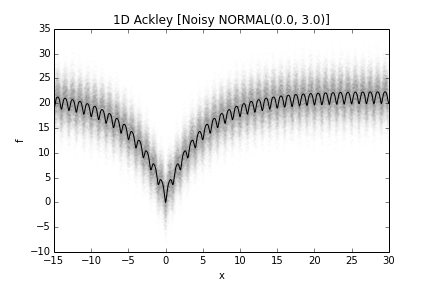
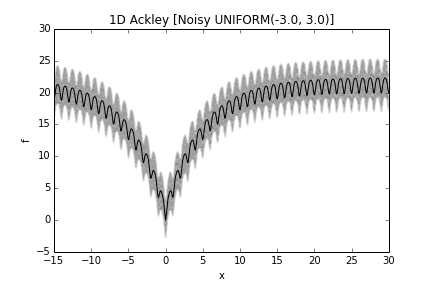
The transformed problem becomes stochastic. It can be solved by optimizers capable of handling stochastic problems, for example pso_gen. The quality of a solution can be assessed by the noise-less version of the problem, serving as the ground truth information.

As some examples, let’s apply pso_gen to different version of noisy problems. Generally, the larger the magnitude of noise, the harder the problem becomes. Increasing the trials parameter reduces the adversarial effect of noise.