Rotated and Shifted problems

In this tutorial we will learn how to use meta-problems. These are optimization problems that transform somehow another optimization problem. In particular we will have a look to the rotated and shifted meta-problems. Let us start creating a shifted problem.

In [1]: from PyGMO import *
In [2]: prob = problem.ackley(5)
In [3]: shifted_prob1 = problem.shifted(problem=prob)
In [4]: shifted_prob2 = problem.shifted(problem=prob,shift=15)
In [5]: shifted_prob3 = problem.shifted(problem=prob,shift=[23,-12.2,22,33,5.3])

We have used three different constructors to instantiate the new problem with a random shift vector (shifted_prob1), with a uniform shift vector (shifted_prob2) and with a fully defined shift vector (shifted_prob3). In all cases we may extract the shift vector using the corresponding attribute

In [4]: shift1 = shifted_prob1.shift_vector
Out[11]: (22.05074397709721, 42.30378775731836, 41.28781073553851, -37.032452729545746, -43.15424830101163)

We may now check that such a shift does not change the performance of a given algorithm. We choose, for this tutorial Improved Harmony Search, but you can try changing it to test others.

In [5]:  l = list()
In [6]:  algo = algorithm.ihs(1000);
In [7]:  for i in range(100):
             pop = population(prob,20)
             for i in range(15):
                 pop = algo.evolve(pop)
             l.append(pop.champion.f[0])
In [8]:  l_shift = list()
In [9]:  for i in range(100):
             pop = population(shifted_prob1,20)
             for i in range(15):
                 pop = algo.evolve(pop)
             l_shift.append(pop.champion.f[0])
In [10]: boxplot([l,l_shift])

which will produce a plot similar to:

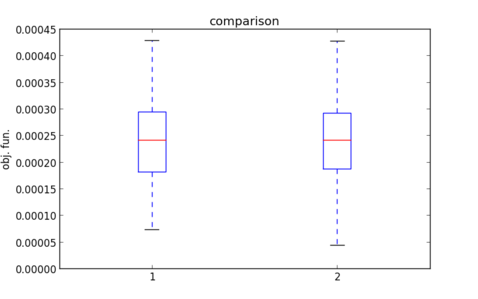
where one can clearly see how the algorithm ihs does not change its performances when the search space is shifted.

We now repeat the same procedure for a rotated problem.

In [1]: from PyGMO import *
In [2]: prob = problem.ackley(5)
In [3]: shifted_prob = problem.rotated(problem=prob)

Also in the case of the rotated problem the kwarg rotation allows to pass a rotation matrix directly, otherwise a random orthonormal matrix will be generated and can be extracted by the problem.rotation attribute.

Running the same procedure as for the shifted problem returns a picture like the one below.

Which clearly indicates how the rotation affects negatively the algorithm performance.

Note that meta-problems can be nested together, so it is perfectly valid to have

In [1]: from PyGMO import *
In [2]: prob = problem.ackley(5)
In [3]: new_prob = problem.rotated(problem.shifted(problem.rotated(prob)))

To make sure one can reconstruct the original problem, the transformations applied are logged in the problem __repr__ method

In [4]: print new_prob
Out[4]:
Problem name: Ackley [Rotated] [Shifted] [Rotated]
     Global dimension:                       5
     Integer dimension:                      0
     Fitness dimension:                      1
     Constraints dimension:                  0
     Inequality constraints dimension:       0
     Lower bounds: [-1.4142135623730951, -1.4142135623730951, -1.4142135623730951, -1.4142135623730951, -1.4142135623730951]
     Upper bounds: [1.4142135623730951, 1.4142135623730951, 1.4142135623730951, 1.4142135623730951, 1.4142135623730951]
     Constraints tolerance:                  0

     Rotation matrix:
-0.599649   0.20824 0.0152832 -0.740073 -0.221622
-0.263871 -0.341942  0.873749  0.072256  0.211634
-0.114375 -0.709787 -0.157299 0.0906273 -0.670943
0.663241  0.209505  0.425168 -0.326385 -0.478461
0.343255 -0.540391  -0.17555 -0.576482  0.476451

     Shift vector: [-2.5281990225671565, 2.2507667730831695, 2.260031719866459, -2.6037537655145679, -0.45739118339223306]


     Rotation matrix:
-0.469888  -0.334498  -0.813054  0.0761044 -0.0216481
-0.416312  -0.467594   0.372853  -0.513315   0.453352
 0.413702  0.0719025  -0.277365   0.149243   0.851161
 0.182474   0.391322  -0.341818  -0.830096 -0.0875853
-0.633596   0.714957  0.0784432   0.139221    0.24871