Ackley

struct ackley

The Ackley problem.

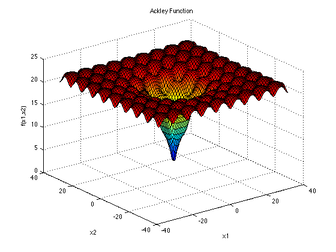
This is a scalable box-constrained continuous single-objective problem. The objective function is the generalised n-dimensional Ackley function:

\[ F\left(x_1,\ldots,x_n\right) = 20 + e - 20e^{-\frac 15 \sqrt{\frac 1n \sum_{i=1}^n x_i^2}} - e^{\frac 1n \sum_{i=1}^n \cos(2\pi x_i)}, \quad x_i \in \left[ -15,30 \right]. \]

The global minimum is in \(x_i=0\), where \( F\left( 0,\ldots,0 \right) = 0 \).

Public Functions

ackley(unsigned dim = 1u)

Constructor from dimension.

Constructs an Ackley problem

Parameters

dim – the problem dimensions.

Throws

std::invalid_argument – if dim is < 1

vector_double fitness(const vector_double&) const

Fitness computation.

Computes the fitness for this UDP

Parameters

x – the decision vector.

Returns

the fitness of x.

std::pair<vector_double, vector_double> get_bounds() const

Box-bounds.

It returns the box-bounds for this UDP.

Returns

the lower and upper bounds for each of the decision vector components

inline std::string get_name() const

Problem name.

Returns

a string containing the problem name

vector_double best_known() const

Optimal solution.

Returns

the decision vector corresponding to the best solution for this problem.

Public Members

unsigned m_dim

Problem dimensions.