Rosenbrock#
-
struct rosenbrock#
The Rosenbrock problem.
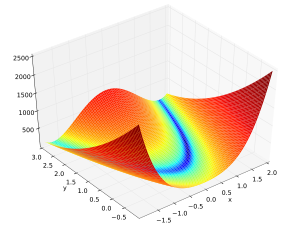
This is a box-constrained continuous single-objective problem. The objective function is the generalised n-dimensional Rosenbrock function:
\[ F\left(x_1,\ldots,x_n\right) = \sum_{i=1}^{n-1}\left[ 100\left(x_i^2-x_{i+1}\right)^2+\left(x_i-1\right)^2\right], \quad x_i \in \left[ -5,10 \right]. \]The global minimum is in \(x_i=1\), where \( F\left( 1,\ldots,1 \right) = 0 \).Public Functions
-
rosenbrock(vector_double::size_type dim = 2u)#
Constructor from dimension.
- Parameters
dim – problem dimension.
- Throws
std::invalid_argument – if
dimis less than 2.
-
vector_double fitness(const vector_double&) const#
Fitness computation.
Computes the fitness for this UDP.
- Parameters
x – the decision vector.
- Returns
the fitness of
x.
-
std::pair<vector_double, vector_double> get_bounds() const#
Box-bounds.
- Returns
the lower (-5.) and upper (10.) bounds for each decision vector component.
-
inline std::string get_name() const#
Problem name.
- Returns
a string containing the problem name.
-
vector_double gradient(const vector_double&) const#
Gradient.
- Parameters
x – the input decision vector.
- Returns
the gradient of the fitness function in
x.
-
vector_double best_known() const#
Optimal solution.
- Returns
the decision vector corresponding to the best solution for this problem.
-
inline thread_safety get_thread_safety() const#
Thread safety level.
- Returns
the
constantthread safety level.
Public Members
-
vector_double::size_type m_dim#
Problem dimensions.
-
rosenbrock(vector_double::size_type dim = 2u)#