Optimal Golomb Ruler#
New in version 2.11.
#include <pagmo/problems/golomb_ruler.hpp>
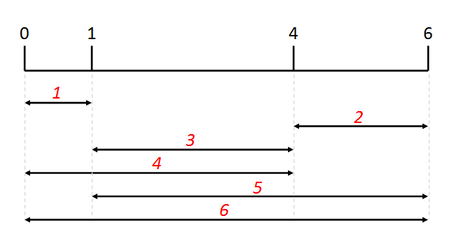
The optimal (and perfect) Golomb ruler of order 4.#
-
class golomb_ruler#
In mathematics, a Golomb ruler is a set of marks at integer positions along an imaginary ruler such that no two pairs of marks are the same distance apart. The number of marks on the ruler is its order, and the largest distance between two of its marks is its length. Translation and reflection of a Golomb ruler are considered trivial, so the smallest mark is customarily put at 0 and the next mark at the smaller of its two possible values. There is no requirement that a Golomb ruler be able to measure all distances up to its length, but if it does, it is called a perfect Golomb ruler.
A Golomb ruler is optimal if no shorter Golomb ruler of the same order exists. Creating Golomb rulers is easy, but finding the optimal Golomb ruler (or rulers) for a specified order is computationally very challenging.
This UDP represents the problem of finding an optimal Golomb ruler of a given order \(n\). A maximal distance \(l_{max}\) between consecutive marks is also specified to make the problem representation possible. The resulting optimization problem is an integer programming problem with one equality constraint.
In this UDP, the decision vector is \(x=[d_1, d_2, d_{n-1}]\), where the distances between consecutive ticks are indicated with \(d_i\). The ticks on the ruler can then be reconstructed as \(a_0 = 0\), \(a_i = \sum_{j=1}^i d_i, i=1 .. n-1\)
Its formulation can thus be written as:
\[\begin{split}\begin{array}{rl} \mbox{find:} & 1 \le d_i \le l_{max}, \forall i=1..n-1 \\ \mbox{to minimize: } & \sum_i d_i \\ \mbox{subject to:} & |a_i-a_j| \neq |a_l - a_m|, \forall (\mbox{distinct}) i,j,l,m \in [0, n] \end{array}\end{split}\]We transcribe the constraints as one single equality constraint: \(c = 0\) where \(c\) is the count of repeated distances.
See: https://en.wikipedia.org/wiki/Golomb_ruler
-
golomb_ruler(unsigned order = 3u, unsigned upper_bound = 10)#
Constructs a UDP representing the search for an optimal Golomb ruler.
- Parameters
order – the ruler order.
upper_bound – maximum distance between consecutive ticks.
- Throws
std::invalid_argument – if order is < 2 or upper_bound is < 1.
std::overflow_error – if upper_bound is too large.
-
vector_double fitness(const vector_double &x) const#
Computes the fitness for this UDP. The complexity is \(n^2\), where \(n^2\) is the ruler order.
- Parameters
x – the decision vector.
- Returns
the fitness of x.
-
vector_double::size_type get_nec() const#
The number of equality constraints of the UDP.
- Returns
the number 1.
-
vector_double::size_type get_nix() const#
The integer dimension of the problem.
- Returns
the ruler order minus 1.
-
std::pair<vector_double, vector_double> get_bounds() const#
Returns the box-bounds for this UDP.
- Returns
the lower and upper bounds for each of the decision vector components.
-
std::string get_name() const#
Returns the problem name.
- Returns
a string containing the problem name: “Golomb Ruler (order order)”.
-
golomb_ruler(unsigned order = 3u, unsigned upper_bound = 10)#