Rastrigin

struct rastrigin

The Rastrigin problem.

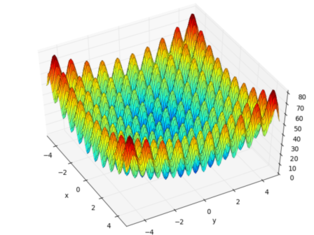
This is a scalable box-constrained continuous single-objective problem. The objective function is the generalised n-dimensional Rastrigin function:

\[ F\left(x_1,\ldots,x_n\right) = 10 \cdot n + \sum_{i=1}^n x_i^2 - 10\cdot\cos\left( 2\pi \cdot x_i \right), \quad x_i \in \left[ -5.12,5.12 \right]. \]

Gradients (dense) are also provided as:

\[ G_i\left(x_1,\ldots,x_n\right) = 2 x_i + 10 \cdot 2\pi \cdot\sin\left( 2\pi \cdot x_i \right) \]

And Hessians (sparse as only the diagonal is non-zero) are:

\[ H_{ii}\left(x_1,\ldots,x_n\right) = 2 + 10 \cdot 4\pi^2 \cdot\cos\left( 2\pi \cdot x_i \right) \]

The global minimum is in the origin, where \( F\left( 0,\ldots,0 \right) = 0 \).

Public Functions

rastrigin(unsigned dim = 1u)

Constructor from dimension.

Constructs a Rastrigin problem

Parameters

dim – the problem dimensions.

Throws

std::invalid_argument – if dim is < 1

vector_double fitness(const vector_double&) const

Fitness computation.

Computes the fitness for this UDP

Parameters

x – the decision vector.

Returns

the fitness of x.

std::pair<vector_double, vector_double> get_bounds() const

Box-bounds.

It returns the box-bounds for this UDP.

Returns

the lower and upper bounds for each of the decision vector components

vector_double gradient(const vector_double&) const

Gradients.

It returns the fitness gradient for this UDP.

The gradient is represented in a sparse form as required by problem::gradient().

Parameters

x – the decision vector.

Returns

the gradient of the fitness function

std::vector<vector_double> hessians(const vector_double&) const

Hessians.

It returns the hessians for this UDP.

The hessians are represented in a sparse form as required by problem::hessians().

Parameters

x – the decision vector.

Returns

the hessians of the fitness function

std::vector<sparsity_pattern> hessians_sparsity() const

Hessians sparsity (only the diagonal elements are non zero)

It returns the hessian sparisty structure for this UDP.

The hessian sparisty is represented in the form required by problem::hessians_sparsity().

Returns

the hessians of the fitness function

inline std::string get_name() const

Problem name.

Returns

a string containing the problem name

vector_double best_known() const

Optimal solution.

Returns

the decision vector corresponding to the best solution for this problem.

Public Members

unsigned m_dim

Problem dimensions.