Using pygmo’s moead

In this tutorial we will see how to use the user-defined algorithm moead provided by pygmo. In particular we will take as test cases problems from the DTLZ suite implemented in pygmo as the user-defined problem dtlz.

The first, quick idea would be to instantiate the problem (say DTLZ1) and run moead with the default settings. We can monitor the convergence of the whole population to the Pareto front using the p_distance() metric.

>>> from pygmo import *
>>> udp = dtlz(prob_id = 1)
>>> pop = population(prob = udp, size = 105)
>>> algo = algorithm(moead(gen = 100))
>>> for i in range(10):
...     pop = algo.evolve(pop)
>>>     print(udp.p_distance(pop)) 
11.906892367806368
5.7957743802958595
5.6155823329927355
5.227825963470699
3.3244186681980863
1.6876728522762465
1.2704673513592113
1.01938844212957
0.9181813093367411
0.6759127264898211

Since the p_distance() does not capture the information on the spread of the solutions we also compute the hypervolume indicator using the pygmo class hypervolume:

>>> hv = hypervolume(pop)
>>> hv.compute(ref_point = [1.,1.,1.]) 

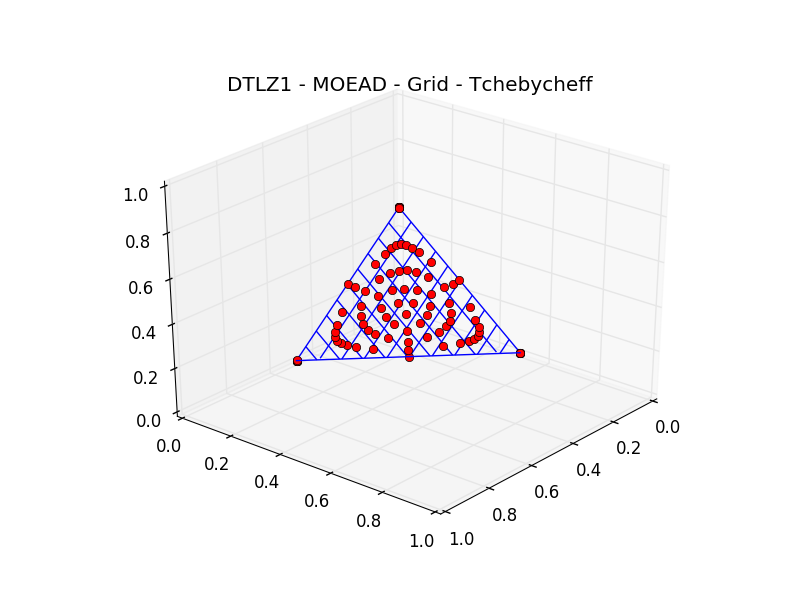
In this case, the reference point can be set manually as the dtlz1 problem is well known. We can also visualize the whole population as the user-defined problem dtlz implements a plot functionality:

>>> from matplotlib import pyplot as plt 
>>> udp.plot(pop) 
>>> plt.title("DTLZ1 - MOEAD - GRID - TCHEBYCHEFF") 

We have used the default parameters of moead in obtaining the results above. In particular the weight_generation kwarg was set to grid and the decomposition kwarg was set to tchebycheff, as can be easily seen inspecting as follows:

>>> print(algo) 
Algorithm name: MOEAD: MOEA/D - DE [stochastic]
    C++ class name: ...

    Thread safety: basic

Extra info:
    Generations: 100
    Weight generation: grid
    Decomposition method: tchebycheff
    Neighbourhood size: 20
    Parameter CR: 1
    Parameter F: 0.5
    Distribution index: 20
    Chance for diversity preservation: 0.9
    Seed: ...
    Verbosity: 0

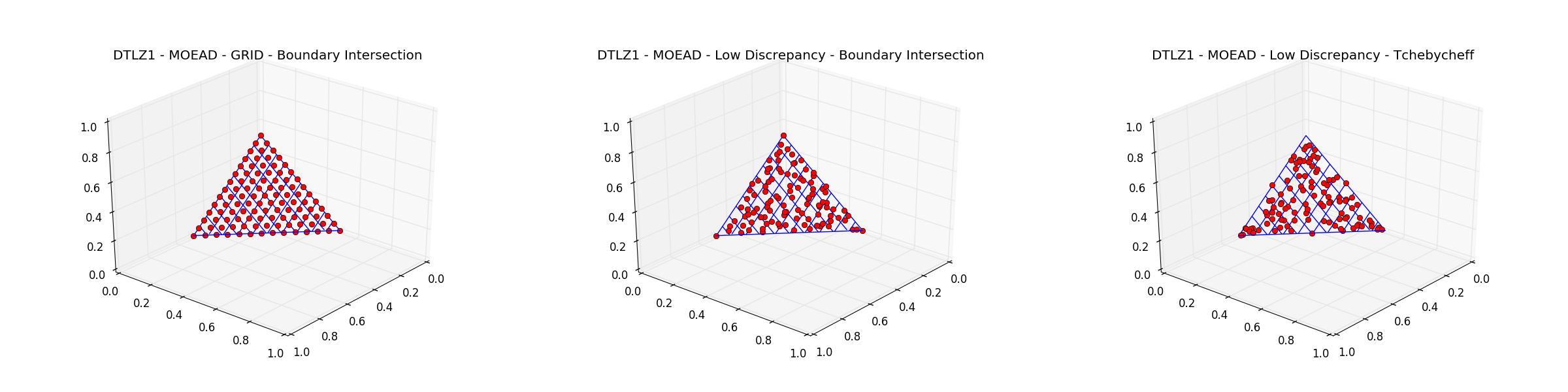
The weight_generation method grid offers a uniform distribution of the decomposed weights, but is limiting the population size as it only allows for certaing sizes according to the number of objectives. This can reveal to be limiting when using moead in comparisons or in other advanced setups. In these cases pygmo provides alternative methods for weight generation. In particular, the original low discrepancy method makes sure that any number of weights can be generated while ensuring a low discrepancy spread over the objective space.

The decomposition method tchebycheff can also be changed as pygmo implements the boundary intersection method too which, when applicable, results in a better spread of the final population over the Pareto front. Repeating the optimization above with different instances of moead results in the plots below.